Questão de Polígonos

por Lucas Garibaldi Ter 24 maio 2022, 08:18

Durante uma aula de artes, os alunos deveriam fazer pinturas que utilizassem figuras geométricas. Bianca fez dois desenhos: um quadrado e um triângulo, ambos regulares, que estavam inscritos em circunferências de mesmo raio, conforme a figura.

Questão de Polígonos 1197_25_325454_3446881_

Sabendo que o perímetro do triângulo pintado por Bianca mede 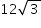Questão de Polígonos Showimage

cm, a medida do lado do quadrado que também foi pintado por ela, em centímetros, é

A
B
C
D

2.
E

4.

por **tales amaral** Ter 24 maio 2022, 10:26

Use lei dos senos no triângulo equilátero para descobrir o dobro do raio. Depois use o fato da diagonal do quadrado ser igual a [latex]2r[/latex] para achar o lado do quadrado.

por **qedpetrich** Ter 24 maio 2022, 10:36

Outra ideia:

Questão de Polígonos Z4CPwX8P0X+kJpu9TeAAAAAAElFTkSuQmCC

Mas sabemos que o apótema de um triângulo equilátero vale 1/3 da altura do triângulo assim:

$Questão de Polígonos Gif$

Continue.

por Lucas Garibaldi Ter 24 maio 2022, 11:06

Olá, qedpetrich, fiz assim, só não sei se fiz corretamente.
l√2 = 2r
l√2 = 8
l = 8/√2
l = 8√2/2
l = 4√2 cm
Alternativa: B

por **qedpetrich** Ter 24 maio 2022, 11:17

Olha, não entendi muito bem como você descobriu o raio. Vou continuar o meu raciocínio. Aplicando um pitágoras no triângulo retângulo formado temos que:

r² = (l/2)² + [(l√3)/6]²
r² = l²/3
r = l√3/3

Do enunciado temos que o perímetro do triângulo equilátero mede 12√3 cm. Assim 3l = 12√3 -> l = 4√3 cm. Substituindo na relação do raio:

r = 4√3.√3/3 = 4.3/3 = 4 cm

Como o colega Tales já nos adiantou, a diagonal do quadrado é 2r, podemos aplicar um novo pitágoras:

8² = L² + L²
64 = 2L²
L = √32 = 4√2 cm

Letra B.