Funções
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Funções
por Vipir2 Ter 07 Dez 2021, 18:43
Seja f: [−3,3] → IR uma função cujo gráfico está representado abaixo.
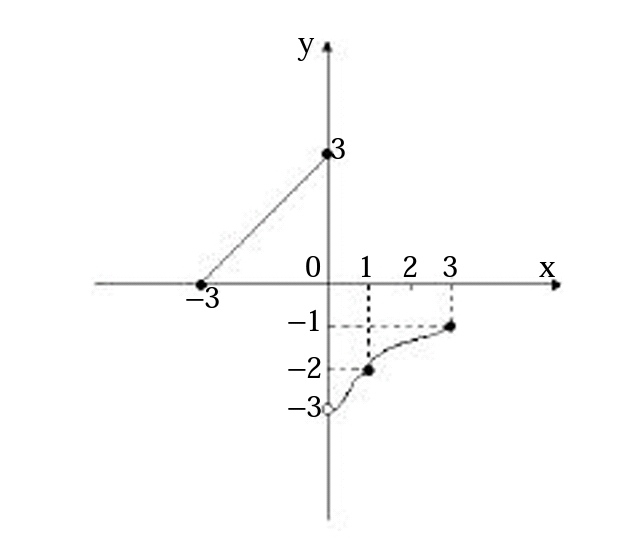
Nessas condições, é correto afirmar que
01) f(−3) = 1.
02) f(−1) = 2.
04) a função f é crescente no intervalo [−3,3].
08) a imagem de f é o intervalo [−3,3].
16) f(inversa)(−1) = 1.
32) (f o f) (0) = −1.
64) (f(inversa) o f) (2) = 2.
Gabarito: 2 + 32 + 64
Nessas condições, é correto afirmar que
01) f(−3) = 1.
02) f(−1) = 2.
04) a função f é crescente no intervalo [−3,3].
08) a imagem de f é o intervalo [−3,3].
16) f(inversa)(−1) = 1.
32) (f o f) (0) = −1.
64) (f(inversa) o f) (2) = 2.
Gabarito: 2 + 32 + 64
Vipir2- Padawan
- Mensagens : 96
Data de inscrição : 30/11/2021
Idade : 18
Re: Funções
por Emanoel Mendonça Ter 07 Dez 2021, 19:15
Boa noite,
01) f(-3) = 0
02) No intervalo do eixo x [-3,0] a função é definida por:
f(x) = x + 3 --> f(-1) = -1 + 3 = 2. OK
04) Para que ela seja considerada crescente nesse intervalo, todos os pontos devem obedecer que:
x1>x2 --> f(x1) > f(x2), sendo x1 e x2 dois pontos quaisquer pertencentes ao gráfico,
vou pegar os pontos (0,3) e (1,-2):
1 > 0 --> verdade
-2 > 3 --> absurdo
As ordenadas não satisfazem a condição.
08) y = -3 não está definido, deveria ser ]-3,3].
16) A inversa será definida pela função: f^-1(x) = x-3
f^-1 (-1) = -1 -3 = -4.
32) Fof = (x+3) +3 = x+6 --> fof(0) = 0+6 = 6
64) f^-1(f(x)) = (x+3)-3 = x --> f^-1(f(2)) = 2. OK
Tem certeza do gabarito ?
01) f(-3) = 0
02) No intervalo do eixo x [-3,0] a função é definida por:
f(x) = x + 3 --> f(-1) = -1 + 3 = 2. OK
04) Para que ela seja considerada crescente nesse intervalo, todos os pontos devem obedecer que:
x1>x2 --> f(x1) > f(x2), sendo x1 e x2 dois pontos quaisquer pertencentes ao gráfico,
vou pegar os pontos (0,3) e (1,-2):
1 > 0 --> verdade
-2 > 3 --> absurdo
As ordenadas não satisfazem a condição.
08) y = -3 não está definido, deveria ser ]-3,3].
16) A inversa será definida pela função: f^-1(x) = x-3
f^-1 (-1) = -1 -3 = -4.
32) Fof = (x+3) +3 = x+6 --> fof(0) = 0+6 = 6
64) f^-1(f(x)) = (x+3)-3 = x --> f^-1(f(2)) = 2. OK
Tem certeza do gabarito ?
Emanoel Mendonça- Fera
- Mensagens : 1744
Data de inscrição : 23/06/2017
Idade : 26
Localização : Resende, RJ, Brasil
tales amaral e Vipir2 gostam desta mensagem
Re: Funções
por Vipir2 Ter 07 Dez 2021, 20:06
A prova era de 1998, imagino que não havia a possibilidade de entrar com recurso, ou não era tão comum. Havia chegado aos mesmos resultados que você, na afirmação 32. Muito obrigado, Emanoel!
Vipir2- Padawan
- Mensagens : 96
Data de inscrição : 30/11/2021
Idade : 18
Re: Funções
por Vipir2 Ter 07 Dez 2021, 20:13
Apenas uma dúvida em relação a determinação da função ser crescente ou decrescente - A regra serve para todos os tipos de função, ou apenas para a do 1º grau?
Vipir2- Padawan
- Mensagens : 96
Data de inscrição : 30/11/2021
Idade : 18
Re: Funções
por tales amaral Ter 07 Dez 2021, 20:18
Creio que a banca seguiu o seguinte raciocínio na 32:
[latex]\left(f \text{ o } f \right ) (0) = f(f(0))[/latex]
Pelo gráfico, [latex]f(0) = 3[/latex] e [latex]f(f(0)) = f(3)[/latex]. Novamente pelo gráfico temos [latex]f(3) = -1[/latex], portanto [latex]f(f(0)) = -1[/latex].
[latex]\left(f \text{ o } f \right ) (0) = f(f(0))[/latex]
Pelo gráfico, [latex]f(0) = 3[/latex] e [latex]f(f(0)) = f(3)[/latex]. Novamente pelo gráfico temos [latex]f(3) = -1[/latex], portanto [latex]f(f(0)) = -1[/latex].
tales amaral- Monitor
- Mensagens : 512
Data de inscrição : 02/05/2020
Idade : 20
Localização : Serra, ES -
Emanoel Mendonça gosta desta mensagem
Vipir2- Padawan
- Mensagens : 96
Data de inscrição : 30/11/2021
Idade : 18
Re: Funções
por Emanoel Mendonça Qua 08 Dez 2021, 14:54
Para todos os tipos de função, se pegarmos um intervalo qualquer seja ela, do 2º,3º... se nesse intervalo a condição for satisfeita, ela será crescente, o que acontece é que a partir da função do 2º a função começa a aparecer ambas características pra determinados intervalos.Vipir2 escreveu:Apenas uma dúvida em relação a determinação da função ser crescente ou decrescente - A regra serve para todos os tipos de função, ou apenas para a do 1º grau?
Emanoel Mendonça- Fera
- Mensagens : 1744
Data de inscrição : 23/06/2017
Idade : 26
Localização : Resende, RJ, Brasil
Re: Funções
por Emanoel Mendonça Qua 08 Dez 2021, 14:56
Obrigado camarada!tales amaral escreveu:Creio que a banca seguiu o seguinte raciocínio na 32:
[latex]\left(f \text{ o } f \right ) (0) = f(f(0))[/latex]
Pelo gráfico, [latex]f(0) = 3[/latex] e [latex]f(f(0)) = f(3)[/latex]. Novamente pelo gráfico temos [latex]f(3) = -1[/latex], portanto [latex]f(f(0)) = -1[/latex].
Emanoel Mendonça- Fera
- Mensagens : 1744
Data de inscrição : 23/06/2017
Idade : 26
Localização : Resende, RJ, Brasil
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
