Áreas

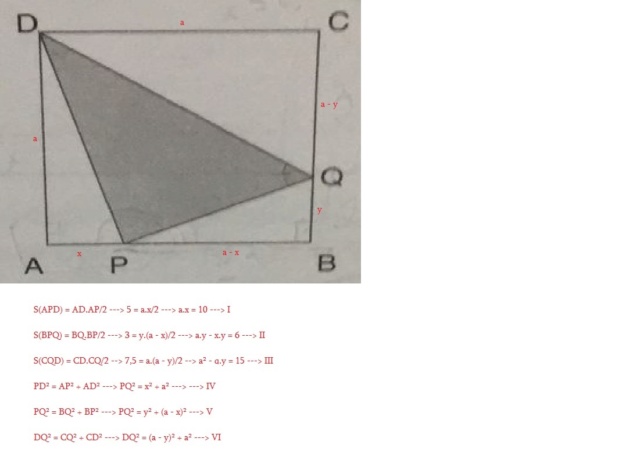
A figura apresenta o quadrado ABCD, cujos lados [latex]\overline{AB}[/latex] e [latex]\overline{BC}[/latex] contêm, respectivamente, os pontos P e Q.


Os segmentos [latex]\overline{PD}[/latex], [latex]\overline{PQ}[/latex] e [latex]\overline{QD}[/latex] dividem esse quadrado em quatro triângulos, de modo que o triângulo:
• APD tem 5cm² de área;
• BPQ tem 3cm² de área;
• CQD tem 7,5cm² de área.

Nessas condições, a área, em cm², do triângulo PQD vale

a) 25,0
b) 15,5
c) 10,0
d) 9,5
e) 6,0

Uma figura e alguns cálculos para ajudar:

nas notações de Elcio,
ax=10
(a-x)y=6
(a-y)a=15

substituindo da primeira na segunda, obtemos
(a-10/a)y=6 -> a²y-6a-10y=0 -> y=6a/(a²-10)
e a²-ay=15 -> y=(a²-15)/a

ent

(a²-15)/a=6a/(a²-10)
-> a⁴-25a²+150=6a²
a⁴-31a²+150=0
resolvendo em a², obtemos
a²=25 ou a²=6. como o ultimo é menor que a soma das areas dos 3 triangulos dados, resta que a²=25
portanto a area do triangulo PQD é a²-DAP-PBQ-DQC=25-5-3-7,5=9,5

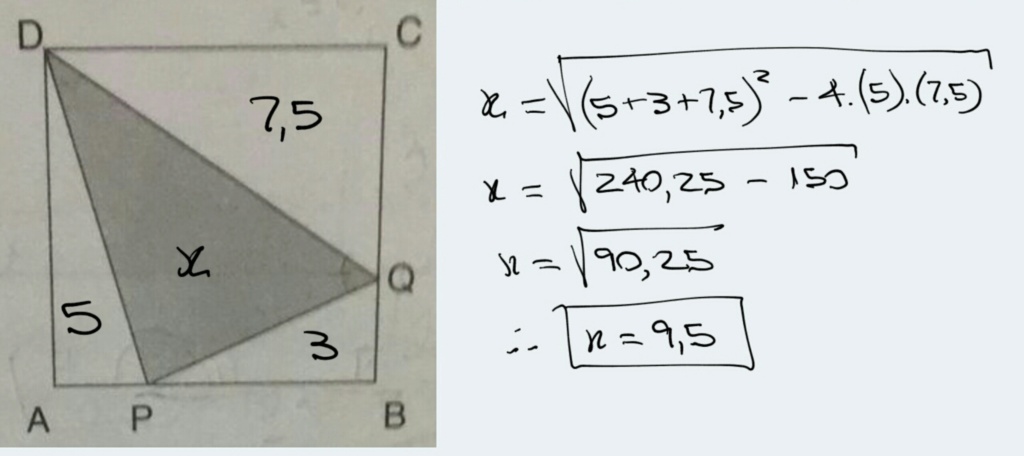
O problema é conhecido. Segue link de duas resoluções distintas deste problema porém ambas com números diferentes deste.

1) https://youtu.be/6K_j4Cj7mVo
neste o autor resolve de forma literal para o caso genérico de um retângulo e obtém a fórmula que usei acima.

2) https://youtu.be/MCvfVqN_0pk
neste o autor resolve de forma criativa e simples diretamente para um quadrado.

______________________________________________________________________________

Raimundo,

não entendi a rotação que você fez nem como pode obter aquela conclusão. Você pode me elucidar?

Acho que tal valeria se DQ fosse bissetriz do ângulo CˆDP, caso em que rotacionaríamos o triângulo ADP em 90º anti-horário -- é conhecido um problema nestes termos. Porém o enunciado não nos autoriza isto.

Medeiros,
O que pensei,
Sabemos que a área de um triâng . pode ser calculada em função do seu perímetro e das medida dos lados.
Se girarmos DPC dentro de ABCD , penso, que a área se mantém, apenas mudam as medidas dos lados. Tratando-se de um quadrado é mantida a proporcionalidade dos lados.
Não olhei os links de resoluções, pq isso me pareceu óbvio.

Ah, Raimundo, você diz dentro do quadrado; então não é rotação do triâng. DPQ, é reflexão. Mesmo porque não daria para rotacionar (com eixo em D, imagino) e continuar dentro do quadrado. Acho que só vou entender quando ver essa situação desenhada.

Medeiros,
Com essa figura espero deixar mais claro o que pensei.
Vou ficar devendo , mas,  não consigo e nem tenho conhecimentos para me aprofundar nesse tema. Abs

Olá, Raimundo.

Obrigado por responder e me esclarecer. Infelizmente só tenho conseguido frequentar o fórum no fim de semana; e gosto de acompanhar criteriosamente suas respostas porque você sempre traz soluções originais, que "pensam fora da caixinha" e que simplificam o trabalho de resolução. Além do que, você estudou muito mais geometria do que eu; leu os livros do Morgado e a Coleção de Matemática Elementar do Iezzi e eu nem sequer tenho esses livros; portanto, normalmente aprendo com você.

Então o que você fez foi reflexão de DPQ em torno da diagonal BD. É perfeitamente válido e mantém a área reflexionada igual a original; e as áreas anexas acima e abaixo trocam de posição (e valor) mas continuam iguais -- até aqui nada demais.

Contudo, desta vez, discordo da sua resolução porque não se pode induzir que BQ = AP, embora o desenho original fique próximo disto e você tenha desenhado estritamente igual. Como você partiu desta premissa, seu resultado foi pura coincidência com o gabarito; tanto é assim que se você usar o mesmo método para resolver o caso com os números que mostrei nos dois links (figura abaixo) irá obter o absurdo de uma área negativa.

Oi Medeiros,
Colocando os Pingos nos Is.
Obrigado pela consideração.
Mas , todos nós sabemos quem realmente é o cacique da Geometria aqui no Pir.
Já falei outras vezes e agradeço até hj, o que vc , mestre Elcio , mestre Euclides, Ivomilton et tantos outros me ajudaram a reaprender a matemática que tinha aprendido há 50 anos. Fato esse decisivo para aprovação dos meus filhos nos vestibulares.
Não estudei, nem estudo esses livros que vc citou , tenho em casa, pq foi deixado pelos filhos e as vezes recorro a eles.
Sobre minhas resoluções, as vezes mais direta.
Primeiro pq optei apenas em colaborar com o Pir (em reconhecimento a tanto que ele me deu), nas resoluções de "alguns" probls de geo. plana, com isso, fico mais concentrado num único tema e mantenho os neurônios ativados. 
Sobre esse prob., eu não induzir , eu considerei duas possibilidades (triângs diferentes , apenas mantendo a mesma medida do vértice do triâng no eixo AB igual no eixo BC. Não fiz , mas acho que ainda poderia fazer mais 2 triângs.
A grande verdade é que o mérito para a resolução desse problema é da pessoa que chegou a fórmula que vc apresentou.Abs