A imagem e o periodo da função f(x) = 2-4 cos(x) são, r

A imagem e o periodo da função f(x) = 2-4 cos(x) são, respectivamente:

a) [-2,6] e π

b) [2, 6] e 2π

c) [-2,6] e 2π

d) [-2,-6] e π


 e) [2,-6] e π

Olá art3mis_17;

Da teoria sabemos que a função cosseno tem como sua imagem variando de [-1,1]. Portanto aplicando na respectiva função:

Máximo de f(x), quando cos(x) = -1 -> f(x) = 2 - 4(-1) = f(x) = 6
Mínimo de f(x), quando cos(x) = 1 -> f(x) = 2 - 4 = f(x) = -2

Imagem -> [-2,6]

Para calcular o período de uma função faz-se o seguinte:

Seja uma função do tipo -> g(x) = a + b . cos(cx + d). Fazendo cx + d = t. Quando x percorre os reais, t percorre os reais também (pois a função afim t = cx + d é sobrejetora) e, em consequência, cos(t) percorre o intervalo [-1,1], como já explicitado, b . cos(t) percorre o intervalo [-b,b] e y = a + b . cos(t) percorre o intervalo [a - b, a + b], que é a imagem de g(x).

Para que g complete um período é necessário que t varie de 0 a 2π, então:





Portanto:



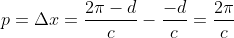
Aplicando os valores, como c = 1, então:



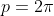
Letra C. Espero ter ajudado!