Soma de cossenos e senos (arcos em P.A.)
3 participantes
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
Soma de cossenos e senos (arcos em P.A.)
por FocoNoITA Sab 04 Set 2021, 20:41
Temos as seguintes somas.
Solucioná-las-ei de duas maneiras.
1⁰ Modo(Números Complexos):
Seja z=cis(θ).
Com isso:
Observe que, do lado esquerdo, obtemos a soma de uma P.G.
Desse modo:
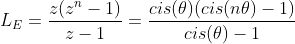
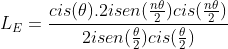
Desse modo, podemos igualar as partes reais e imaginárias:
Também:
2⁰Modo(Trigonometria):
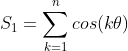
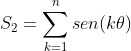
Expandindo S₁:
Utilizando as fórmulas de transformação de produto em soma, obtemos:
A resolução de S₂ é análoga à de S₁.
Observe que os resultados, dos dois modos, são as mesmas coisas, só estão escritos de formas diferentes.
Solucioná-las-ei de duas maneiras.
1⁰ Modo(Números Complexos):
Seja z=cis(θ).
Com isso:
Observe que, do lado esquerdo, obtemos a soma de uma P.G.
Desse modo:
Desse modo, podemos igualar as partes reais e imaginárias:
Também:
2⁰Modo(Trigonometria):
Expandindo S₁:
Utilizando as fórmulas de transformação de produto em soma, obtemos:
A resolução de S₂ é análoga à de S₁.
Observe que os resultados, dos dois modos, são as mesmas coisas, só estão escritos de formas diferentes.
FocoNoITA- Jedi
- Mensagens : 251
Data de inscrição : 05/05/2020
Idade : 20
Localização : São José dos Campos, São Paulo, Brasil
Giovana Martins, eduardodudu101, Rory Gilmore, BatataLaranja345, matheusbon e Marcim gostam desta mensagem
Re: Soma de cossenos e senos (arcos em P.A.)
por eduardodudu101 Sab 04 Set 2021, 23:32
Muito bom! Eu conhecia apenas a demonstração por complexos.
eduardodudu101- Jedi
- Mensagens : 219
Data de inscrição : 15/07/2017
Idade : 20
Localização : Porto Velho,Rondônia,Brasil
FocoNoITA gosta desta mensagem
Soma de cossenos e senos (arcos em P.A.)
por Giovana Martins Dom 13 Fev 2022, 11:00
Uma possível demonstração para soma de cossenos e senos cujos arcos estão em progressão aritmética.
[latex]\mathrm{Sejam\ as\ somas:\left\{\begin{matrix} \mathrm{1+cos(x)+cos(2x)+cos(3x)+...+cos(nx)}\\ \mathrm{sin(x)+sin(2x)+sin(3x)+...+sin(nx)} \end{matrix}\right.}[/latex]
[latex]\mathrm{Sejam:\left\{\begin{matrix}
\mathrm{iS=isin(x)+isin(2x)+isin(3x)+...+isin(nx)}\\
\mathrm{C=1+cos(x)+cos(2x)+cos(3x)+...+cos(nx)}
\end{matrix}\right.}[/latex]
[latex]\mathrm{C+iS=1+cos(x)+isin(x)+cos(2x)+isin(2x)+...+cos(nx)+isin(nx)}[/latex]
[latex]\mathrm{C+iS=1+e^{ix}+e^{2ix}+...+e^{nix}}[/latex]
[latex]\mathrm{Sendo\ e^{ix}=a\ e\ considerando:1+a+a^2+a^3+...a^n=\frac{a^{n+1}-1}{a-1}}[/latex]
[latex]\mathrm{Logo:C+iS=1+e^{ix}+(e^{ix})^2+(e^{ix})^3+...+(e^{ix})^n=1+a+a^2+a^3+...+a^n=\frac{{(e^{ix})^{n+1}}-1}{e^{ix}-1}}[/latex]
[latex]\mathrm{C+iS=\frac{{(e^{ix})^{n+1}}-1}{e^{ix}-1}=\frac{e^{\frac{ix(n+1)}{2}}}{e^{\frac{ix}{2}}}\left [ \frac{e^{\frac{ix(n+1)}{2}}-e^{-\frac{ix(n+1)}{2}}}{e^{\frac{ix}{2}}-e^{-\frac{ix}{2}}} \right ]}[/latex]
[latex]\mathrm{Por\ def.:sin\left [ \frac{x(n+1)}{2} \right ]=\frac{e^{\frac{ix(n+1)}{2}}-e^{-\frac{ix(n+1)}{2}}}{2i}}[/latex]
[latex]\mathrm{Logo:C+iS=\frac{2isin\left [ \frac{x(n+1)}{2} \right ]}{2isin\left ( \frac{x}{2} \right )}e^{i\left [ \frac{x(n+1)}{2}-\frac{x}{2} \right ]}=\frac{sin\left [ \frac{x(n+1)}{2} \right ]}{sin\left ( \frac{x}{2} \right )}e^{i\left ( \frac{xn}{2} \right )}=\frac{sin\left [ \frac{x(n+1)}{2} \right ]}{sin\left ( \frac{x}{2} \right )}cis\left ( \frac{xn}{2} \right )}[/latex]
[latex]\mathrm{Comparando:C=\frac{sin\left [ \frac{x(n+1)}{2} \right ]cos\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}\ e\ S=\frac{sin\left [ \frac{x(n+1)}{2} \right ]sin\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}}[/latex]
[latex]\mathrm{\therefore 1+cos(x)+cos(2x)+cos(3x)+...+cos(nx)=\frac{sin\left [ \frac{x(n+1)}{2} \right ]cos\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}}[/latex]
[latex]\mathrm{\therefore sin(x)+sin(2x)+sin(3x)+...+sin(nx)=\frac{sin\left [ \frac{x(n+1)}{2} \right ]sin\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}}[/latex]
Fonte: Trigonometria Plana y Esferica e Introducción al Cálculo.
Nota¹: se notarem algum erro, avisem. Escrever essas expressões em LaTeX é bem desagradável
.
Nota²: postei esta demonstração, pois é relativamente comum postarem questões deste estilo no nosso fórum.
[latex]\mathrm{Sejam\ as\ somas:\left\{\begin{matrix} \mathrm{1+cos(x)+cos(2x)+cos(3x)+...+cos(nx)}\\ \mathrm{sin(x)+sin(2x)+sin(3x)+...+sin(nx)} \end{matrix}\right.}[/latex]
[latex]\mathrm{Sejam:\left\{\begin{matrix}
\mathrm{iS=isin(x)+isin(2x)+isin(3x)+...+isin(nx)}\\
\mathrm{C=1+cos(x)+cos(2x)+cos(3x)+...+cos(nx)}
\end{matrix}\right.}[/latex]
[latex]\mathrm{C+iS=1+cos(x)+isin(x)+cos(2x)+isin(2x)+...+cos(nx)+isin(nx)}[/latex]
[latex]\mathrm{C+iS=1+e^{ix}+e^{2ix}+...+e^{nix}}[/latex]
[latex]\mathrm{Sendo\ e^{ix}=a\ e\ considerando:1+a+a^2+a^3+...a^n=\frac{a^{n+1}-1}{a-1}}[/latex]
[latex]\mathrm{Logo:C+iS=1+e^{ix}+(e^{ix})^2+(e^{ix})^3+...+(e^{ix})^n=1+a+a^2+a^3+...+a^n=\frac{{(e^{ix})^{n+1}}-1}{e^{ix}-1}}[/latex]
[latex]\mathrm{C+iS=\frac{{(e^{ix})^{n+1}}-1}{e^{ix}-1}=\frac{e^{\frac{ix(n+1)}{2}}}{e^{\frac{ix}{2}}}\left [ \frac{e^{\frac{ix(n+1)}{2}}-e^{-\frac{ix(n+1)}{2}}}{e^{\frac{ix}{2}}-e^{-\frac{ix}{2}}} \right ]}[/latex]
[latex]\mathrm{Por\ def.:sin\left [ \frac{x(n+1)}{2} \right ]=\frac{e^{\frac{ix(n+1)}{2}}-e^{-\frac{ix(n+1)}{2}}}{2i}}[/latex]
[latex]\mathrm{Logo:C+iS=\frac{2isin\left [ \frac{x(n+1)}{2} \right ]}{2isin\left ( \frac{x}{2} \right )}e^{i\left [ \frac{x(n+1)}{2}-\frac{x}{2} \right ]}=\frac{sin\left [ \frac{x(n+1)}{2} \right ]}{sin\left ( \frac{x}{2} \right )}e^{i\left ( \frac{xn}{2} \right )}=\frac{sin\left [ \frac{x(n+1)}{2} \right ]}{sin\left ( \frac{x}{2} \right )}cis\left ( \frac{xn}{2} \right )}[/latex]
[latex]\mathrm{Comparando:C=\frac{sin\left [ \frac{x(n+1)}{2} \right ]cos\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}\ e\ S=\frac{sin\left [ \frac{x(n+1)}{2} \right ]sin\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}}[/latex]
[latex]\mathrm{\therefore 1+cos(x)+cos(2x)+cos(3x)+...+cos(nx)=\frac{sin\left [ \frac{x(n+1)}{2} \right ]cos\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}}[/latex]
[latex]\mathrm{\therefore sin(x)+sin(2x)+sin(3x)+...+sin(nx)=\frac{sin\left [ \frac{x(n+1)}{2} \right ]sin\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}}[/latex]
Fonte: Trigonometria Plana y Esferica e Introducción al Cálculo.
Nota¹: se notarem algum erro, avisem. Escrever essas expressões em LaTeX é bem desagradável
. Nota²: postei esta demonstração, pois é relativamente comum postarem questões deste estilo no nosso fórum.
Giovana Martins- Grande Mestre
- Mensagens : 6206
Data de inscrição : 15/05/2015
Idade : 22
Localização : São Paulo
@Khan@, Leonardo Mariano e gabriel_balbao gostam desta mensagem
Re: Soma de cossenos e senos (arcos em P.A.)
por FocoNoITA Dom 13 Fev 2022, 15:38
Giovana Martins escreveu:Uma possível demonstração para soma de cossenos e senos cujos arcos estão em progressão aritmética.
[latex]\mathrm{Sejam\ as\ somas:\left\{\begin{matrix} \mathrm{1+cos(x)+cos(2x)+cos(3x)+...+cos(nx)}\\ \mathrm{sin(x)+sin(2x)+sin(3x)+...+sin(nx)} \end{matrix}\right.}[/latex]
[latex]\mathrm{Sejam:\left\{\begin{matrix}
\mathrm{iS=isin(x)+isin(2x)+isin(3x)+...+isin(nx)}\\
\mathrm{C=1+cos(x)+cos(2x)+cos(3x)+...+cos(nx)}
\end{matrix}\right.}[/latex]
[latex]\mathrm{C+iS=1+cos(x)+isin(x)+cos(2x)+isin(2x)+...+cos(nx)+isin(nx)}[/latex]
[latex]\mathrm{C+iS=1+e^{ix}+e^{2ix}+...+e^{nix}}[/latex]
[latex]\mathrm{Sendo\ e^{ix}=a\ e\ considerando:1+a+a^2+a^3+...a^n=\frac{a^{n+1}-1}{a-1}}[/latex]
[latex]\mathrm{Logo:C+iS=1+e^{ix}+(e^{ix})^2+(e^{ix})^3+...+(e^{ix})^n=1+a+a^2+a^3+...+a^n=\frac{{(e^{ix})^{n+1}}-1}{e^{ix}-1}}[/latex]
[latex]\mathrm{C+iS=\frac{{(e^{ix})^{n+1}}-1}{e^{ix}-1}=\frac{e^{\frac{ix(n+1)}{2}}}{e^{\frac{ix}{2}}}\left [ \frac{e^{\frac{ix(n+1)}{2}}-e^{-\frac{ix(n+1)}{2}}}{e^{\frac{ix}{2}}-e^{-\frac{ix}{2}}} \right ]}[/latex]
[latex]\mathrm{Por\ def.:sin\left [ \frac{x(n+1)}{2} \right ]=\frac{e^{\frac{ix(n+1)}{2}}-e^{-\frac{ix(n+1)}{2}}}{2i}}[/latex]
[latex]\mathrm{Logo:C+iS=\frac{2isin\left [ \frac{x(n+1)}{2} \right ]}{2isin\left ( \frac{x}{2} \right )}e^{i\left [ \frac{x(n+1)}{2}-\frac{x}{2} \right ]}=\frac{sin\left [ \frac{x(n+1)}{2} \right ]}{sin\left ( \frac{x}{2} \right )}e^{i\left ( \frac{xn}{2} \right )}=\frac{sin\left [ \frac{x(n+1)}{2} \right ]}{sin\left ( \frac{x}{2} \right )}cis\left ( \frac{xn}{2} \right )}[/latex]
[latex]\mathrm{Comparando:C=\frac{sin\left [ \frac{x(n+1)}{2} \right ]cos\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}\ e\ S=\frac{sin\left [ \frac{x(n+1)}{2} \right ]sin\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}}[/latex]
[latex]\mathrm{\therefore 1+cos(x)+cos(2x)+cos(3x)+...+cos(nx)=\frac{sin\left [ \frac{x(n+1)}{2} \right ]cos\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}}[/latex]
[latex]\mathrm{\therefore sin(x)+sin(2x)+sin(3x)+...+sin(nx)=\frac{sin\left [ \frac{x(n+1)}{2} \right ]sin\left ( \frac{xn}{2} \right )}{sin\left ( \frac{x}{2} \right )}}[/latex]
Fonte: Trigonometria Plana y Esferica e Introducción al Cálculo.
Nota¹: se notarem algum erro, avisem. Escrever essas expressões em LaTeX é bem desagradável
Nota²: postei esta demonstração, pois é relativamente comum postarem questões deste estilo no nosso fórum.
Boa Tarde! Tudo bem?
Essa demonstração já existe no fórum:
https://pir2.forumeiros.com/t185728-somatorios-trigonometricos
FocoNoITA- Jedi
- Mensagens : 251
Data de inscrição : 05/05/2020
Idade : 20
Localização : São José dos Campos, São Paulo, Brasil
Giovana Martins gosta desta mensagem
Re: Soma de cossenos e senos (arcos em P.A.)
por Giovana Martins Dom 13 Fev 2022, 16:42
Boa tarde, FocoNoITA! Tudo ótimo! Espero que você esteja bem também.
Obrigada por avisar. Irei unir nossas postagens em um único post.
Obrigada por avisar. Irei unir nossas postagens em um único post.
Giovana Martins- Grande Mestre
- Mensagens : 6206
Data de inscrição : 15/05/2015
Idade : 22
Localização : São Paulo
FocoNoITA gosta desta mensagem
Tópicos semelhantes» Trigonometria - Soma de Senos e Cossenos.
» Lei dos senos e lei dos cossenos
» Lei dos Senos e Cossenos
» Lei dos senos e cossenos
» Lei dos senos e lei dos cossenos
» Lei dos senos e lei dos cossenos
» Lei dos Senos e Cossenos
» Lei dos senos e cossenos
» Lei dos senos e lei dos cossenos
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
