Razão entre áreas

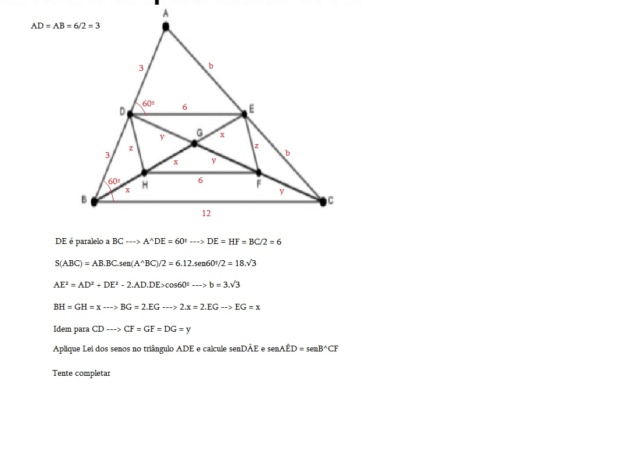
Do triângulo ABC abaixo têm-se os seguintes dados: 

- AB --6m
-BC = 12m 
- ABC= 60° (ângulo em b)

-G é ponto de intersecção das medianas CD e BE.

 - H e F são pontos médios de BG e CG, respectivamente.

A razão entre as áreas do triângulo ABC e do quadrilátero DEFH é, em m2




Consegui apenas a área do triângulo que foi 18raizde3

Gab:3

prolegômenos
Tracemos a mediana AM, obviamente passando por G (baricentro de ABC).

Considere o triâng. BCG; nele F e H são pontos médios, logo FH // BC. Como D e E são pontos médios no triâng. ABC, também DE // BC e DE = BC/2 = 6. Portanto FH // DE // BC e FH = 6.

O quadrilátero DEFH é um paralelogramo cujas diagonais se cruzam no ponto G. As diagonais de um paralelogramo o dividem em quatro áreas de mesma medida, logo [GDE] = [GEF] = [GFH] = [GHD] = (1/4).[DEFG].

Falta explicitar porque DH e EF são paralelas de modo a formar um paralelogramo em DEFH. Considere o triângulo ABG; nele D e H são pontos médios dos lados AB e BG respectivamente, portanto DH // AG. Analogamente, para o triângulo ACG, temos que EF // AG. Portanto, pela propriedade transitiva, DH // EF // AG.

Obrigado, mestres. Vou tentar fazer com todos esses conselhos. Vocês são feras!

perfeito, Raimundo, acho esta solução muito mais elegante.

Eu também tinha pensado em uma forma parecida, que sequer fazia uso das medidas de lados e ângulo dadas no enunciado -- desnecessárias pois pede-se apenas uma relação entre as áreas e não para as calcular -- mas deixei daquele modo só para usar os números dados. Depois coloco aqui o outro modo.

conforme tinha me comprometido, outro modo também elegante e com exposição bem esmiuçada. Mas se vc prestar atenção notará que não se faz contas, apenas a relação: 4 vezes 1/4 de 1/3 de um valor genérico S.

seja:
S = área do triângulo ABC
S' = área do quadrilátero DEFH
e queremos saber S/S' = ?

DE é base média do triângulo ABC pois que D e E são pontos médios, logo

HF é base média do triângulo BCG pois H e F são pontos médios, logo

de (1) e (2) temos que ---> HF//DE e HF = DE = BC/2 ..................................... (3)
de (3) podemos concluir que ---> DH//EF e DH = EF (pelo princípio do rema-rema de balanço) ............................ (4)
portanto, de (3) e (4), o quadrilátero DEFH é um paralelogramo ....................... (5)

O ponto G é encontro de duas medianas, portanto G é baricentro d triângulo ABC. Os segmentos que ligam o baricentro aos vértices fividem o triângulo em três áreas de mesma medida. Portanto

No triângulo BCG, devido a (2) e a semelhança,

(6) em (7) ---> S_HFG = (1/4).(1/3).S ................................. (8)

Como DF e EH são diagonais do paralelogramo DEFH que se encontram no ponto G, temos que:
a) G também é baricentro de DEFH;
b) as diagonais dividiram o paralelogramo em quatro áreas de mesma medida, logo

(8) em (9) ---> S' = 4.(1/4).(1/3).S -----> S' = (1/3).S -----> S/S' = 3