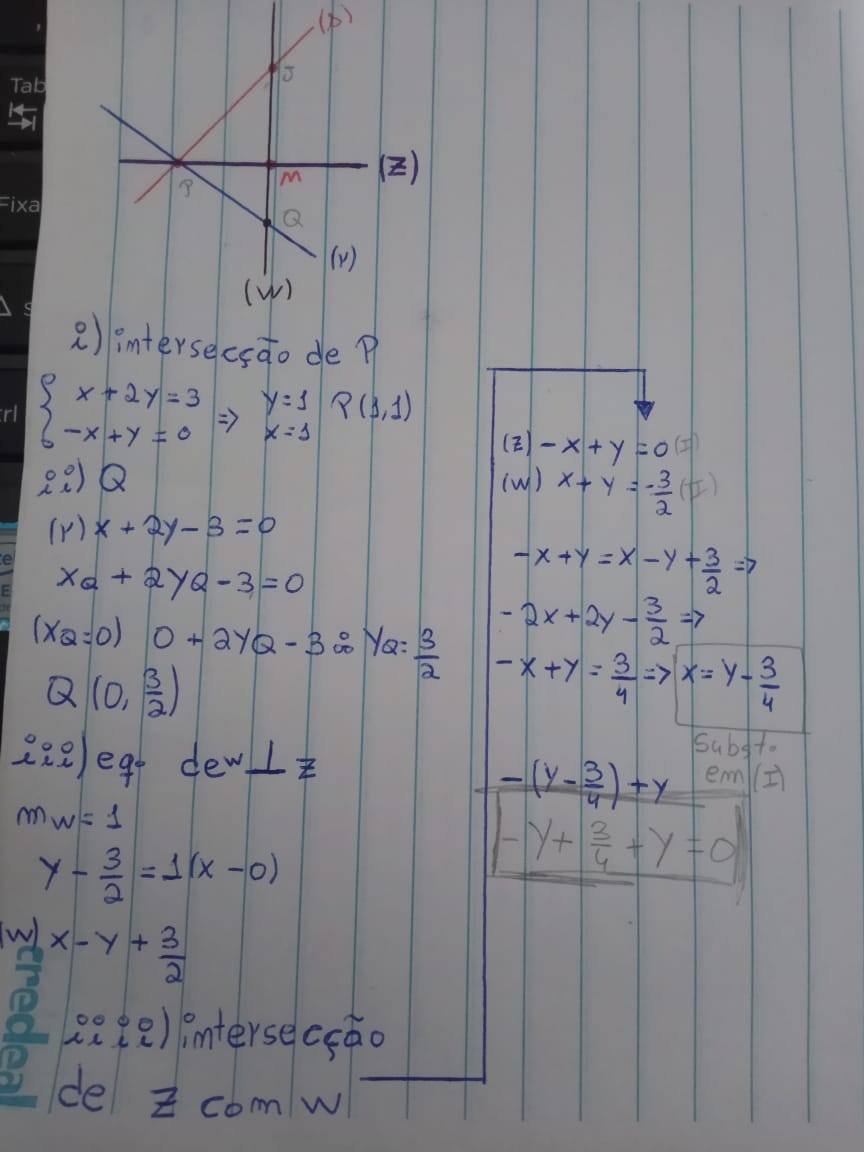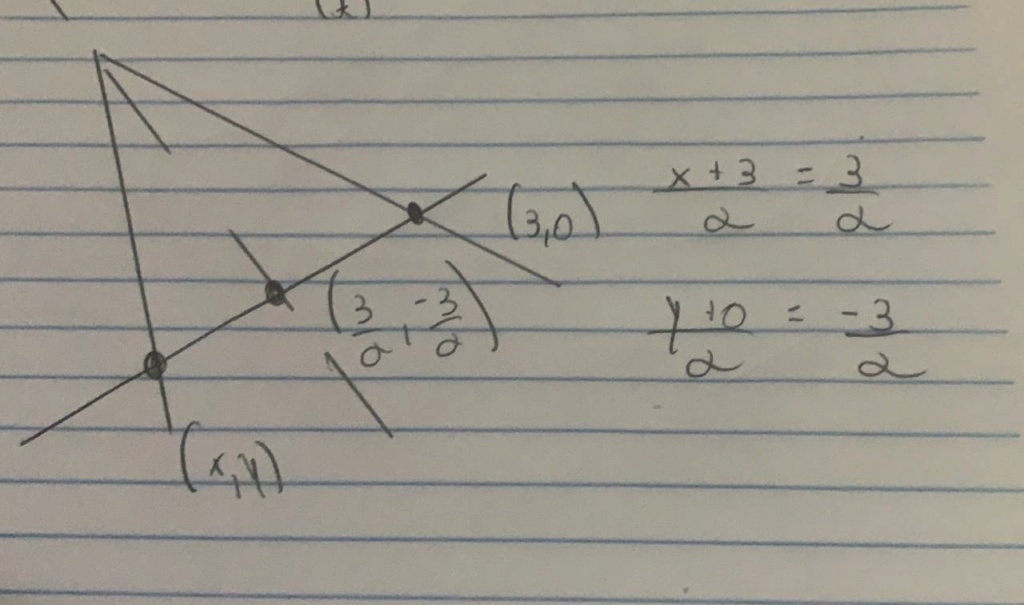Geometria Analítica, FME
3 participantes
Página 1 de 1
 Geometria Analítica, FME
Geometria Analítica, FME
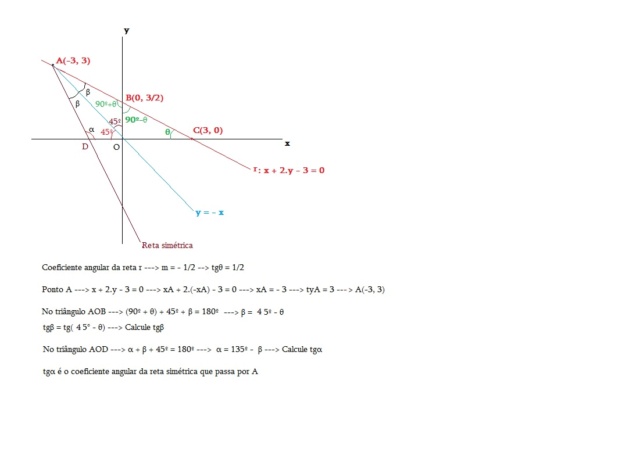
Determinar a equação da reta s simétrica da reta (r) x+ 2y - 3 = 0 em relação à bissetriz do 2° quadrante:
O gabarito é: 2x + y + 3
Cheguei ao resultado de 2x + 7y - 9. Mesmo revendo meus cálculos não achei o erro. Há um tópico bem parecido com este no fórum, mas não entendi a explicação.
Alguém poderia me explicar o passo a passo desta questão ? Desde já, agradeço!
O gabarito é: 2x + y + 3
Cheguei ao resultado de 2x + 7y - 9. Mesmo revendo meus cálculos não achei o erro. Há um tópico bem parecido com este no fórum, mas não entendi a explicação.
Alguém poderia me explicar o passo a passo desta questão ? Desde já, agradeço!
Última edição por IvanGomes067 em Qui 29 Abr 2021, 21:44, editado 1 vez(es)

IvanGomes067- Iniciante
- Mensagens : 39
Data de inscrição : 07/11/2020
Idade : 24
Localização : Natal, RN, Brasil
 Re: Geometria Analítica, FME
Re: Geometria Analítica, FME
Poste sua resolução, vou tentar ver qual ideia você fez errado ou qual conta.
____________________________________________
''I have nothing to offer but blood, toil, tears and sweat''
Sir Winston Churchill

MarioCastro- Elite Jedi

- Mensagens : 274
Data de inscrição : 20/04/2019
Idade : 21
Localização : Rio de Janeiro, RJ

IvanGomes067- Iniciante
- Mensagens : 39
Data de inscrição : 07/11/2020
Idade : 24
Localização : Natal, RN, Brasil
 Re: Geometria Analítica, FME
Re: Geometria Analítica, FME
Poderia me explicar um passo a passo desta questão ? Estou com bastante dificuldade nesse tópico de Geometria Analítica.

IvanGomes067- Iniciante
- Mensagens : 39
Data de inscrição : 07/11/2020
Idade : 24
Localização : Natal, RN, Brasil
 Re: Geometria Analítica, FME
Re: Geometria Analítica, FME
Você começou errando na reta bissetriz do Segundo quadrante, a reta seria
x + y = 0
Vou tentar fazer um passo a passo pra ti, mas suponho que ficará grande
x + y = 0
Vou tentar fazer um passo a passo pra ti, mas suponho que ficará grande
____________________________________________
''I have nothing to offer but blood, toil, tears and sweat''
Sir Winston Churchill

MarioCastro- Elite Jedi

- Mensagens : 274
Data de inscrição : 20/04/2019
Idade : 21
Localização : Rio de Janeiro, RJ
IvanGomes067 gosta desta mensagem
 Re: Geometria Analítica, FME
Re: Geometria Analítica, FME
Primeira etapa é analisar as retas no plano cartesiano :
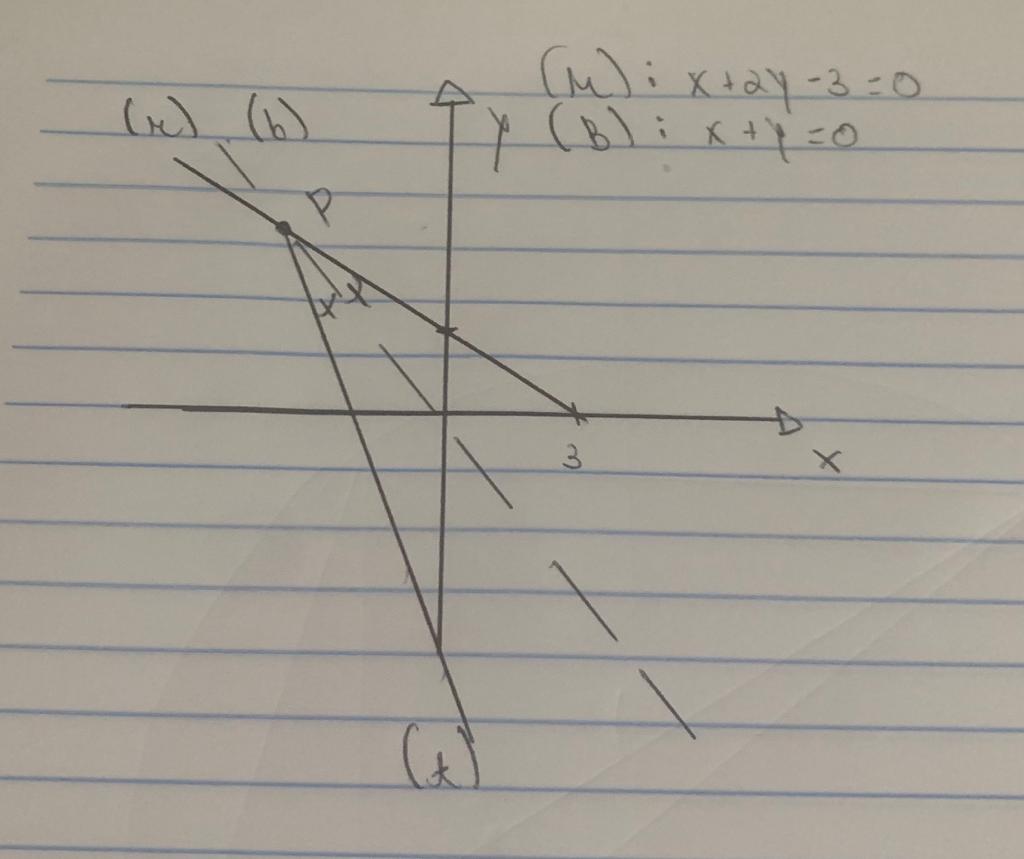
Chamaremos a reta bissetriz do segundo quadrante de (b)
A reta que nos foi dada de (s)
A que queremos achar de (t)
A perpendicular que teremos que traçar de (v)
O ponto P que você citou é o ponto comum às três retas ( t, s, b)
Para acharmos a equação de uma reta precisamos de 2 pontos dela, ou de um ponto e a tangente dela. Eu acho a equação de uma reta pela determinante de 2 pontos. Ex:
A reta que passa pelos pontos (3,0) e (2,3). Não vou ensinar, pois acredito que por você estar nesse capítulo do FME já tenha passado pelo tópico de criação de retas e equação geral da reta. Mas caso não saiba me de um alerta que eu te ensino.
Voltando :
Com o ponto P nós já identificaremos um ponto que passa sobre a reta (t), falta mais um ponto para identificarmos ela.
Basta fazer a interseção das retas (s) e (b) que vai encontrar o ponto
P(-3 , 3 )
Segundo passo é traçar uma reta transversal à reta (s) que passe pela reta (t) e (r) como na figura a seguir :
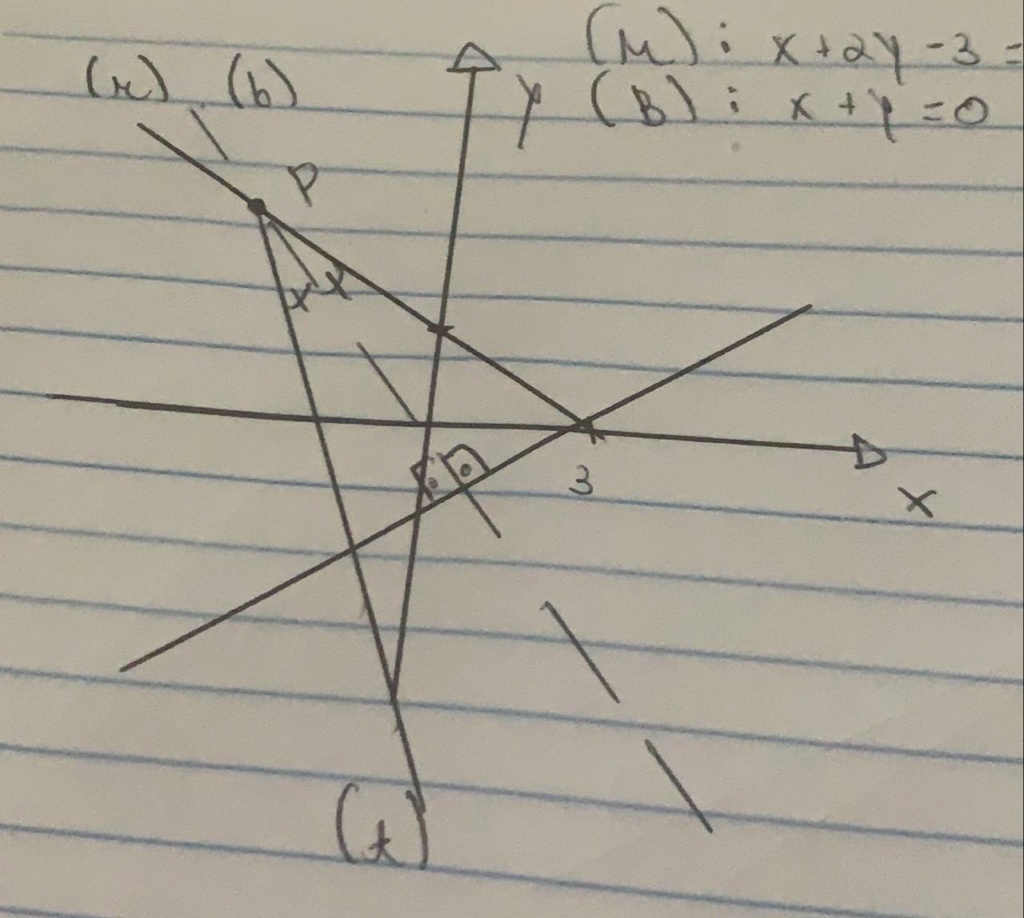
Vamos supor que essa reta transversal (v) passe por um ponto genérico da reta (r), pode usar qualquer ponto mas eu vou usar o ponto (3,0)
Você tem que identificar a reta (v) agora, temos que ela passa pelo ponto genérico (3,0) e o coeficiente angular dela é 1 ( creio que já tenha estudado coeficiente angulares, mas pode mandar uma mensagem caso não tenha entendido.)
A reta (v) ficaria assim : (y - 0) = 1.(x - 3)
(v) : x - y - 3 =0
Assim a interseção entre (v) e (b) é o ponto Z (3/2 , -3/2)
Esse ponto Z é médio dos outros pontos pertencentes à reta (t) e (r), pois se fecha um triângulo isósceles, onde a reta de referência é a bissetriz e altura (mediana por consequência) de um dos lados. (Esse triângulo não é por acaso, é devidamente planejado.)...........

Chamaremos a reta bissetriz do segundo quadrante de (b)
A reta que nos foi dada de (s)
A que queremos achar de (t)
A perpendicular que teremos que traçar de (v)
O ponto P que você citou é o ponto comum às três retas ( t, s, b)
Para acharmos a equação de uma reta precisamos de 2 pontos dela, ou de um ponto e a tangente dela. Eu acho a equação de uma reta pela determinante de 2 pontos. Ex:
A reta que passa pelos pontos (3,0) e (2,3). Não vou ensinar, pois acredito que por você estar nesse capítulo do FME já tenha passado pelo tópico de criação de retas e equação geral da reta. Mas caso não saiba me de um alerta que eu te ensino.
Voltando :
Com o ponto P nós já identificaremos um ponto que passa sobre a reta (t), falta mais um ponto para identificarmos ela.
Basta fazer a interseção das retas (s) e (b) que vai encontrar o ponto
P(-3 , 3 )
Segundo passo é traçar uma reta transversal à reta (s) que passe pela reta (t) e (r) como na figura a seguir :

Vamos supor que essa reta transversal (v) passe por um ponto genérico da reta (r), pode usar qualquer ponto mas eu vou usar o ponto (3,0)
Você tem que identificar a reta (v) agora, temos que ela passa pelo ponto genérico (3,0) e o coeficiente angular dela é 1 ( creio que já tenha estudado coeficiente angulares, mas pode mandar uma mensagem caso não tenha entendido.)
A reta (v) ficaria assim : (y - 0) = 1.(x - 3)
(v) : x - y - 3 =0
Assim a interseção entre (v) e (b) é o ponto Z (3/2 , -3/2)
Esse ponto Z é médio dos outros pontos pertencentes à reta (t) e (r), pois se fecha um triângulo isósceles, onde a reta de referência é a bissetriz e altura (mediana por consequência) de um dos lados. (Esse triângulo não é por acaso, é devidamente planejado.)...........
____________________________________________
''I have nothing to offer but blood, toil, tears and sweat''
Sir Winston Churchill

MarioCastro- Elite Jedi

- Mensagens : 274
Data de inscrição : 20/04/2019
Idade : 21
Localização : Rio de Janeiro, RJ
IvanGomes067 gosta desta mensagem
 Re: Geometria Analítica, FME
Re: Geometria Analítica, FME
____________________________________________
''I have nothing to offer but blood, toil, tears and sweat''
Sir Winston Churchill

MarioCastro- Elite Jedi

- Mensagens : 274
Data de inscrição : 20/04/2019
Idade : 21
Localização : Rio de Janeiro, RJ
IvanGomes067 gosta desta mensagem

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
IvanGomes067 gosta desta mensagem
 Re: Geometria Analítica, FME
Re: Geometria Analítica, FME
Mario, do fundo do meu coração, muito obrigado por ter feito uma explicação tão detalhada. Fiquei uns bons três dias tentando entender esse assunto e sua resolução foi ponto chave para isso. Obrigado, novamente!
Agradeço também ao mestre Elcio, a resolução postado pelo senhor iluminou minhas ideias!
Abraços.
Agradeço também ao mestre Elcio, a resolução postado pelo senhor iluminou minhas ideias!
Abraços.

IvanGomes067- Iniciante
- Mensagens : 39
Data de inscrição : 07/11/2020
Idade : 24
Localização : Natal, RN, Brasil
MarioCastro gosta desta mensagem
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos