Relação de Stewart
3 participantes
Página 1 de 1
Relação de Stewart
por ruanramos Qua 14 Abr 2021, 18:32
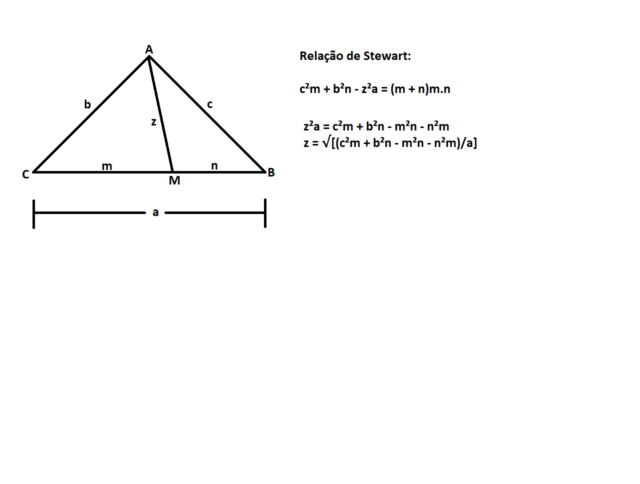
Dados os lados a, b e c de um triangulo ABC, calcular a distância do vértice A ao ponto M que divide a base BC em segmentos proporcionais a m e n.
gab [latex]\frac{\sqrt{{m}^{2}{c}^{2} + {n}^{2}{b}^{2} + mn ({c}^{2} + {b}^{2} -{a}^{2})}}{m+n}[/latex]
Segue minha resolução, se alguém puder ver o que estou fazendo de errado, não chego no gabarito dado, desde já agradeço.
gab [latex]\frac{\sqrt{{m}^{2}{c}^{2} + {n}^{2}{b}^{2} + mn ({c}^{2} + {b}^{2} -{a}^{2})}}{m+n}[/latex]
Segue minha resolução, se alguém puder ver o que estou fazendo de errado, não chego no gabarito dado, desde já agradeço.
ruanramos- Recebeu o sabre de luz
- Mensagens : 131
Data de inscrição : 02/06/2020
Idade : 22
Localização : São Paulo
ruanramos- Recebeu o sabre de luz
- Mensagens : 131
Data de inscrição : 02/06/2020
Idade : 22
Localização : São Paulo
Resposta
por dolino26/2 Qui 02 Fev 2023, 11:17
Provavelmente ele não irá ver isso, mas vou deixar aqui caso alguém esteja procurando por essa questão...
Ruan, sua solução está correta, porém você só esqueceu de radicalizar a expressão.
Partindo da sua expressão ---->
a = m + n; sendo assim:
multiplicando o numerador e o denominador por:
teremos:
multiplicando os dois termos do numerador teremos:
agora colocando mn em evidência ainda no numerador, teremos:
percebe-se, através do produto notável a^2+2ab+b^2=(a+b)^2 que:
então:
como dito anteriormente, m+n = a, ou seja:
Espero ter ajudado alguém.
Ótimo dia a todos...
Ruan, sua solução está correta, porém você só esqueceu de radicalizar a expressão.
Partindo da sua expressão ---->
a = m + n; sendo assim:
multiplicando o numerador e o denominador por:
teremos:multiplicando os dois termos do numerador teremos:
agora colocando mn em evidência ainda no numerador, teremos:
percebe-se, através do produto notável a^2+2ab+b^2=(a+b)^2 que:
então:como dito anteriormente, m+n = a, ou seja:
Espero ter ajudado alguém.
Ótimo dia a todos...
dolino26/2- Iniciante
- Mensagens : 1
Data de inscrição : 02/02/2023
Medeiros gosta desta mensagem
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tópicos semelhantes» Relação de Stewart
» Teorema de Stewart
» Relação de Stewart para Cevianas
» Stewart
» teorema de stewart
» Teorema de Stewart
» Relação de Stewart para Cevianas
» Stewart
» teorema de stewart
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
