Lugar Geométrico
3 participantes
Página 1 de 1
 Lugar Geométrico
Lugar Geométrico
:(Cesgranrio)No triângulo ABC, são dados os vértices B e C e também a medida do ângulo A, agudo. O lugar geométrico do vértice A é:
a) uma circunferência.
b) um arco de circunferência.
c) a união de dois arcos de circunferências.
d) uma reta.
e) a união de duas retas paralelas.
resposta:[C]
a) uma circunferência.
b) um arco de circunferência.
c) a união de dois arcos de circunferências.
d) uma reta.
e) a união de duas retas paralelas.
resposta:[C]

Tomaz1- Recebeu o sabre de luz

- Mensagens : 168
Data de inscrição : 12/10/2020
Idade : 21
 Re: Lugar Geométrico
Re: Lugar Geométrico
que diabo de enunciado mais mal escrito!
Primeiro que se foi dado o triângulo ABC então, obviamente, já estão dados seus três vértices: são o A, o B e o C.
Com certeza o L.G. do vértice A é uma circunferência pois TODO triângulo é inscritível.
Porém SE o enunciado dissesse: "no triângulo ABC são fixados os vértices B e C e dada suas distâncias até o vértice A; então o L.G. do vértice A é:". Aqui neste caso, sim, a resposta é o item c, interseção de dois arcos de circunferência. Note que não tem importância alguma a informação sobre o tipo de ângulo do vértice A -- pode ser agudo, obtuso ou reto, só não pode ser raso.
Primeiro que se foi dado o triângulo ABC então, obviamente, já estão dados seus três vértices: são o A, o B e o C.
Com certeza o L.G. do vértice A é uma circunferência pois TODO triângulo é inscritível.
Porém SE o enunciado dissesse: "no triângulo ABC são fixados os vértices B e C e dada suas distâncias até o vértice A; então o L.G. do vértice A é:". Aqui neste caso, sim, a resposta é o item c, interseção de dois arcos de circunferência. Note que não tem importância alguma a informação sobre o tipo de ângulo do vértice A -- pode ser agudo, obtuso ou reto, só não pode ser raso.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
humildedaturmaita gosta desta mensagem
 Re: Lugar Geométrico
Re: Lugar Geométrico
Se for, então, como comedidamente diz o Élcio, temos as posições fixas de dois vértices (B e C), a medida do ângulo  e queremos definir a posição do vértice A.
O lugar geométrico (L.G.) do vértice A é o arco capaz de ° do segmento BC. O Euclides já mostrou aqui como construir esse arco e agora vou repetir.
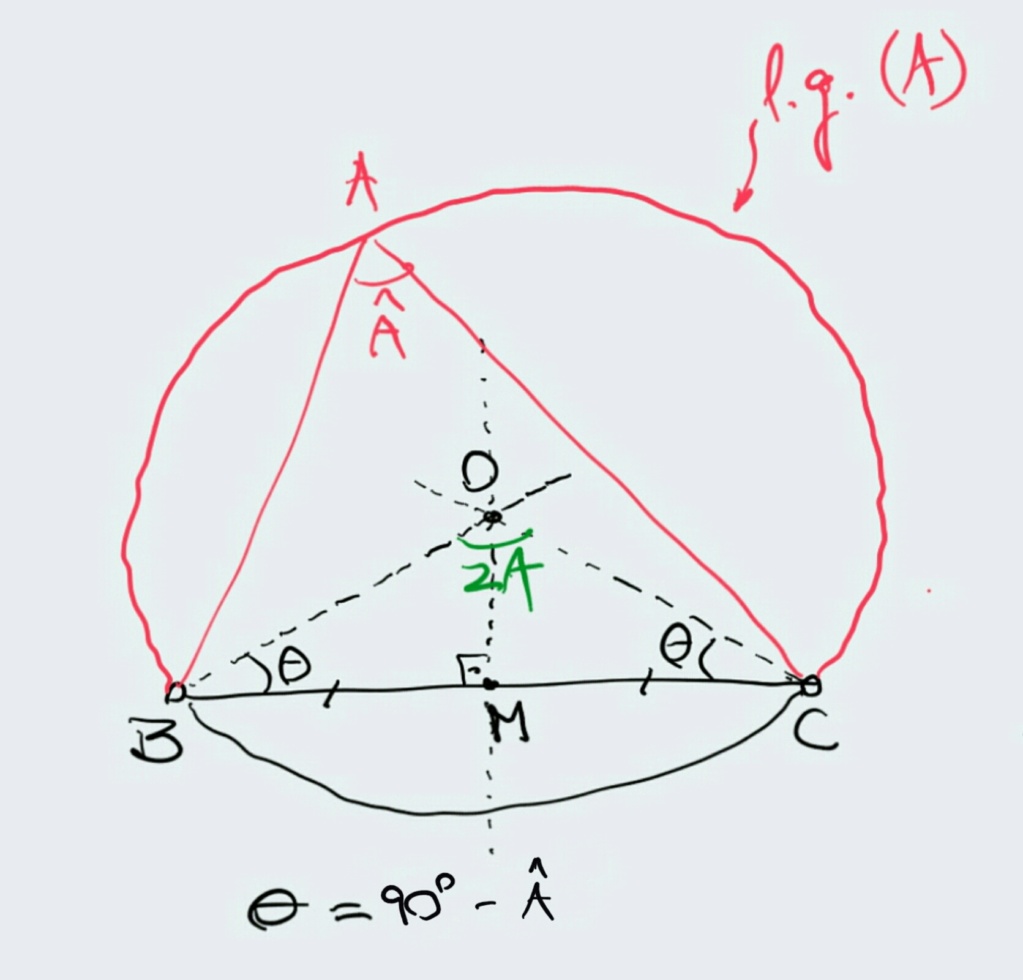
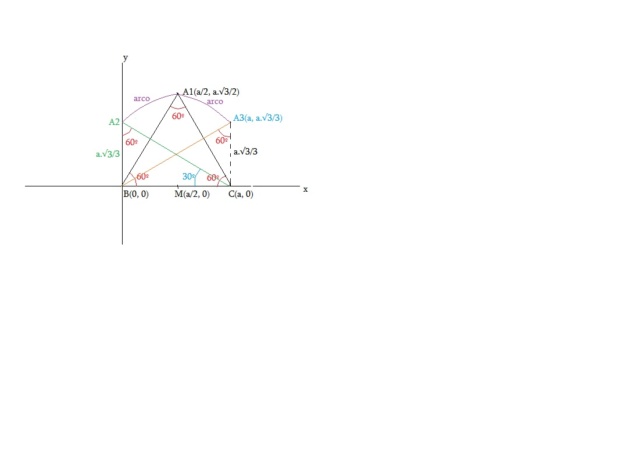
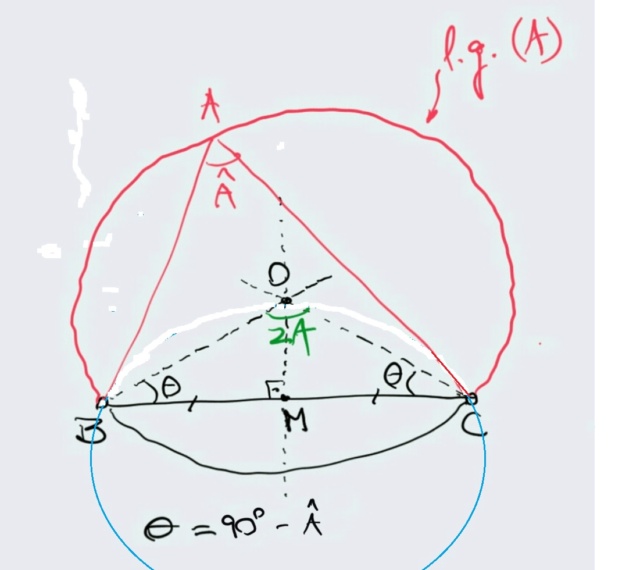
1) traçamos a mediatriz do segmento BC (M é o ponto médio de BC).
2) queremos um ângulo central igual a 2Â. Para isso, em B (ou em C) construímos um ângulo (90° - Â) e traçamos um segmento de B até encontrar a mediatriz no ponto O. Não é necessário mas por didática tracei o segmento CO, que é igual a BO. Resulta que o ângulo BÔC = 2Â.
3) Com centro em O e raio OB (= OC) traçamos o arco de circunferência BC no semiplano que contém o centro (em vermelho).
Este arco em vermelho é o arco capaz de ° do segmento BC e, consequentemente, é o pedido lugar geométrico do vértice A, pois como o ângulo central mede 2 (por construção) qualquer ângulo inscrito neste arco mede a metade do central, ou seja, o dado ângulo Â.
Nesta situação a resposta é item b) um arco de circunferência e, de novo, não bate com o gabarito.
atenção: nesta construção, qualquer ângulo partindo do arco em preto que completa a circunferência NÃO mede Â, ele é o suplementar do ângulo Â.
O lugar geométrico (L.G.) do vértice A é o arco capaz de ° do segmento BC. O Euclides já mostrou aqui como construir esse arco e agora vou repetir.

1) traçamos a mediatriz do segmento BC (M é o ponto médio de BC).
2) queremos um ângulo central igual a 2Â. Para isso, em B (ou em C) construímos um ângulo (90° - Â) e traçamos um segmento de B até encontrar a mediatriz no ponto O. Não é necessário mas por didática tracei o segmento CO, que é igual a BO. Resulta que o ângulo BÔC = 2Â.
3) Com centro em O e raio OB (= OC) traçamos o arco de circunferência BC no semiplano que contém o centro (em vermelho).
Este arco em vermelho é o arco capaz de ° do segmento BC e, consequentemente, é o pedido lugar geométrico do vértice A, pois como o ângulo central mede 2 (por construção) qualquer ângulo inscrito neste arco mede a metade do central, ou seja, o dado ângulo Â.
Nesta situação a resposta é item b) um arco de circunferência e, de novo, não bate com o gabarito.
atenção: nesta construção, qualquer ângulo partindo do arco em preto que completa a circunferência NÃO mede Â, ele é o suplementar do ângulo Â.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Lugar Geométrico
Re: Lugar Geométrico
É verdade, Élcio. Muito bem observado.
É possível construir dois arcos capazes, um em cada semiplano da reta BC.
Mancada minha não perceber isso. E vergonha minha meu comportamento arrogante em culpar o enunciado por não ter percebido seu alcance. O pior é que conheço e concordo com a filosofia do "antes de dizer não dá, pense num modo de conseguir"; e não fiz isto.
Obrigado pela correção, pela resposta completa e por restabelecer a verdade de que o gabarito está correto.
É possível construir dois arcos capazes, um em cada semiplano da reta BC.
Mancada minha não perceber isso. E vergonha minha meu comportamento arrogante em culpar o enunciado por não ter percebido seu alcance. O pior é que conheço e concordo com a filosofia do "antes de dizer não dá, pense num modo de conseguir"; e não fiz isto.
Obrigado pela correção, pela resposta completa e por restabelecer a verdade de que o gabarito está correto.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos