ITA 2012

Acredita-se que a colisão de um grande asteróide com a Terra tenha causado a extinção dos dinossauros. Para se ter uma ideia de um impacto dessa ordem, considere um asteróide esférico de ferro, com 2km de diâmetro, que se encontra em repouso quase no infinito, estando sujeito somente à ação da gravidade terrestre. Desprezando as forças de atrito atmosférico, assinale a opção que expressa a energia liberada no impacto, medida em número aproximado de bombas de hidrogênio de 10 megatons de TNT. A) 1 B) 10 C) 500 D) 50.000 E) 1.000.000

resposta: D

A prova de Física do ITA 2012 traz que:
1 ton de TNT = 4,0x10^(9) J.
Aceleração da gravidade g = 10 m/s².
Massa específica do ferro ρ = 8000 kg/m³.
Raio da Terra R = 6400 km.

E sabendo que:
g = GM/R²
gR²/G = M (I)

Conservando a energia no infinito e na superfície terrestre:
Ec = GMm/R

De (I):
Ec = GgR²m/(GR)
Ec = gRm (II)

g = 10 m/s²
R = 6400 km

m = Vρ
m = 4πr³ρ/3
m = 4π*(1x10³)³*8000/3
m ≈ 3,2x10^(13) kg (arredondando π pra 3, já que a questão pede uma aproximação)

Aplicando os dados supracitados em negrito em (II):
Ec ≈ 10*6,4x10^(6)*3,2x10^(13)
Ec ≈ 2x10^(21) J

Sabendo, do enunciado, que 1 ton de TNT libera 4x10^(9) J, se tem que 10 megatons (10^(7)) liberarão:
4x10^(9)*10^(7) = 4x10^(16) J

Realizando a relação solicitada pela questão, enfim se obtém:
2x10^(21)/[(4x10^(16)] = 50.000

Alternativa D.

Mas Christhian, por que o R da fórmula Epotencial = - Ec = -GMm/R foi considerado como sendo o raio da Terra?


É justamente isso que eu não entendo. 


A energia potencial não é em relação à distância do objeto (asteroide) ao outro centro de massa (Terra)? Esse R não deveria ser a distância da Terra ao asteroide? (afinal, é essa energia potencial entre eles que se converte em cinética)
E essa distância não é o infinito; pois, como diz o enunciado: "[o asteroide] se encontra em repouso quase no infinito". 
Dessa maneira, eu penso que a energia potencial que é transformada em cinética é em relação à distancia infinita que o asteroide se encontrava inicialmente da Terra. E com isso não entendo o porque de usar-se o raio da terra no R da fórmula. Porque, ao fazermos isso [usarmos o raio da terra no R da fórmula] estamos considerando que a energia potencial que se transforma em cinética é SÓ a energia potencial do asteroide na superfície da Terra em relação ao centro de massa da Terra. Assim, estaríamos descartando a energia potencial que o asteroide tinha armazenado por estar muuuito além da superfície terrestre.

A energia mecânica foi conservada do infinito até à superfície terrestre.

No infinito, era dada por:
E = -GMm/d + mv0²/2 = 0 (já que d = ∞ e v0 = 0)
Onde d = distância entre os centros de massa da terra e do asteroide.

Na Terra, é dada por:
E = Ec + (- GMm/R)

Igualando ambas:
0 = Ec - GMm/R
Ec = GMm/R

Lembrando que a energia potencial gravitacional de um corpo situado no infinito em relação a um outro corpo, é nula. Por isso E = - GMm/d² + mv²/2 = 0.

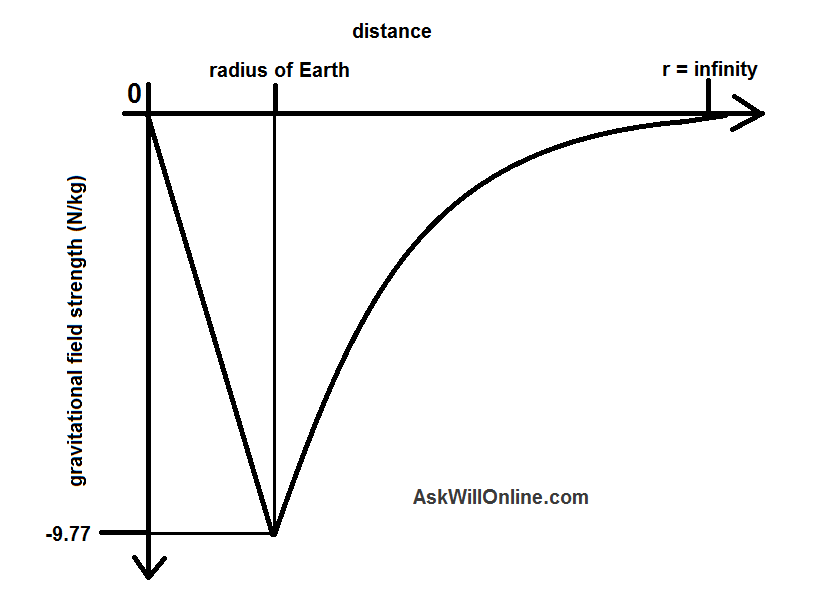
obs: o gráfico está invertido, ele na verdade é negativo