ITA(2014)-(modificada)
2 participantes
Página 1 de 1
ITA(2014)-(modificada)
por Annie Qua 12 Ago 2020, 17:08
Classifique a afirmação:
Sejam a, b, c ∈ [latex]\mathbb{R}[/latex] , com a < b < c. Se f:[a, c] → [a, b] é sobrejetora, então f não é injetora.
Sejam a, b, c ∈ [latex]\mathbb{R}[/latex] , com a < b < c. Se f:[a, c] → [a, b] é sobrejetora, então f não é injetora.
Última edição por Annie em Qua 12 Ago 2020, 19:07, editado 1 vez(es)
Annie- Iniciante
- Mensagens : 11
Data de inscrição : 19/04/2019
Re: ITA(2014)-(modificada)
por Vitor Ahcor Qua 12 Ago 2020, 18:41
Olá,
A afirmação é falsa. Um contra exemplo no qual f é injetiva e sobrejetiva:
A afirmação é falsa. Um contra exemplo no qual f é injetiva e sobrejetiva:
____________________________________________
Cha-la head-cha-la
Vitor Ahcor- Monitor
- Mensagens : 750
Data de inscrição : 21/12/2018
Idade : 23
Localização : São José dos Campos
Annie gosta desta mensagem
Re: ITA(2014)-(modificada)
por Annie Qua 12 Ago 2020, 19:01
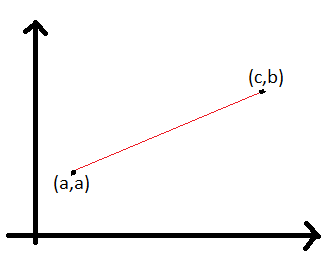
Estou com certa dificuldade em entender por que essa função é injetiva visto que o intervalo referente ao domínio da função[a, c] é maior do que o seu contradomínio [a, b].
As funções injetivas devem possuir apenas 1 elemento correspondente do contradomínio.
As funções injetivas devem possuir apenas 1 elemento correspondente do contradomínio.
Annie- Iniciante
- Mensagens : 11
Data de inscrição : 19/04/2019
Vitor Ahcor gosta desta mensagem
Re: ITA(2014)-(modificada)
por Vitor Ahcor Qua 12 Ago 2020, 19:08
Annie, o conjunto dos números reais é não enumerável, você não pode pensar naquele diagrama de conjuntos com as flechas. O melhor modo de perceber que é possível existir f, é pelo desenho que fiz.
____________________________________________
Cha-la head-cha-la
Vitor Ahcor- Monitor
- Mensagens : 750
Data de inscrição : 21/12/2018
Idade : 23
Localização : São José dos Campos
Annie gosta desta mensagem
Tópicos semelhantes» DNA-UPE ( MODIFICADA )
» (ITA - Modificada) - Polinômios
» UDESC(Modificada)
» FUVEST - Modificada
» UDESC - Modificada
» (ITA - Modificada) - Polinômios
» UDESC(Modificada)
» FUVEST - Modificada
» UDESC - Modificada
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
