ufrgs cv 2014 inequações no plano cartesiano - Q32
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 ufrgs cv 2014 inequações no plano cartesiano - Q32
ufrgs cv 2014 inequações no plano cartesiano - Q32
Construídas no mesmo sistema de coordenadas cartesianas, as inequações x² + y² < 4 e y < x + 1 delimitam uma região no plano. O número de pontos que estão no interior dessa região e possuem coordenadas inteiras é
a) 5
b) 6
c) 7
d) 8
e) 9
Qual conteúdo tenho que estudar para aprender a resolver esse tipo de questão? Sempre me perco nele
a) 5
b) 6
c) 7
d) 8
e) 9
Qual conteúdo tenho que estudar para aprender a resolver esse tipo de questão? Sempre me perco nele
Última edição por folettinhomed em Qua 25 Set 2019, 18:52, editado 1 vez(es)

folettinhomed- Mestre Jedi

- Mensagens : 988
Data de inscrição : 23/02/2019
Idade : 24
Localização : Santa Cruz do Sul, RS, Brasil
 Re: ufrgs cv 2014 inequações no plano cartesiano - Q32
Re: ufrgs cv 2014 inequações no plano cartesiano - Q32
x^2 + y^2 < 4
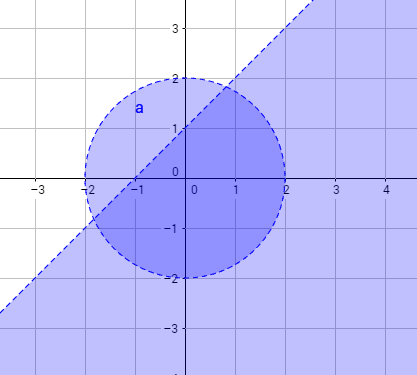
Temos aqui um círculo de raio 2, certo? Estamos pintando círculos concêntricos de raio menor do que 2. É geometria analítica
Agora fazemos y < x + 1. Escolha valores de "x" quaisquer. Note que, para que a inequação seja verdadeira, o "y" será sempre menor do que x + 1. Então pintamos abaixo da linha.
Agora conte quantas coordenadas inteiras estão pintadas na intersecção.
Temos aqui um círculo de raio 2, certo? Estamos pintando círculos concêntricos de raio menor do que 2. É geometria analítica
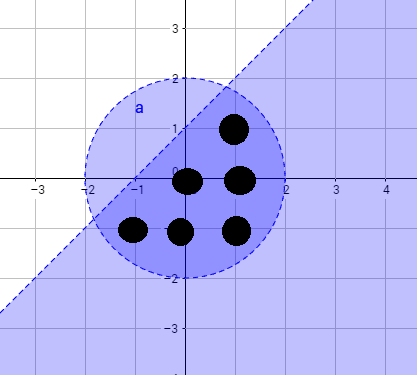
Agora fazemos y < x + 1. Escolha valores de "x" quaisquer. Note que, para que a inequação seja verdadeira, o "y" será sempre menor do que x + 1. Então pintamos abaixo da linha.
Agora conte quantas coordenadas inteiras estão pintadas na intersecção.


Mathematicien- Mestre Jedi

- Mensagens : 668
Data de inscrição : 14/08/2014
 Tópicos semelhantes
Tópicos semelhantes» Plano Cartesiano T-76 FME-1
» Plano cartesiano
» Plano Cartesiano
» f (x) e g (x) no plano cartesiano
» Plano cartesiano
» Plano cartesiano
» Plano Cartesiano
» f (x) e g (x) no plano cartesiano
» Plano cartesiano
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












