Retas e Áreas

A equação de uma reta que é paralela à reta x-2y+3=0 e que determina com as retas x-y=0 e x+y=0 um triângulo de área igual a 12 é:

RESPOSTA: x-2y-6=0

Bom, primeiro eu encontrei o coeficiente angular da reta que se procura, que é 1/2. Depois eu vi que as outras duas retas formam um ângulo de 90 graus, e portanto, o triângulo formado seria retângulo, mas depois disso não consigo desenvolver. Tentei usar base vezes altura do triângulo mas fica muito complicado. Se alguém puder ajudar eu agradeço.

Desenhe as retas do enunciado, em escala

Reta r ---> x - 2.y + 3 = 0 ---> y = (1/2).x + 3/2 ---> m = 1/2

Reta s, paralela a reta r ---> y = (1/2).x + k ---> passa por A(-2.k, 0) ---> vértice do triângulo

Vértice B ----> B(0, 0)
Vértice C é o ponto de encontro da reta s com a reta x + y = 0 ---> y = - x:

- xC = (1/2).xC + k ---> (3/2).x = - k ---> xC = -2.k/3 ---> yC = 2.k/3

Área de ABC --->S = (xB - xA).yC/2

Mas Elcio, quando ele diz que a reta faz um triângulo com as outras duas retas, ele não está falando sobre o triângulo 1?

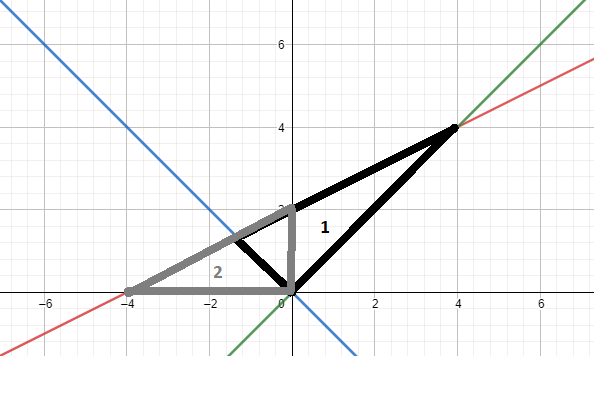
Coloquei as retas y=x e y=-x, e então usei de exemplo a reta y=(x/2) + k, com k = 2. Eu fiz a questão achando que o triângulo 1 era oque ele pedia, mas na sua resolução você calcula a área do triângulo 2 não é?

E se S=(xB-xA)yC/2, teríamos:
S=((0-(-2K))2K/3)/2
Como S=12
24=2K*2K/3
K²=18, K=√ 18

y=(x/2)+K
y=(x/2)+√ 18
E essa fórmula para a reta não bate com o gabarito

Seu desenho não atende o enunciado:

Reta r: x - 2y + 3 = 0 passa por (-3, 0) e (0, 3/2) ---> Não vejo esta reta no desenho

Não vejo também a reta s paralela a reta r (por exemplo, um pouco acima dela)

Um dos lados do triângulo está sobre a reta y = 0 (eixo x)

O segundo lado está sobre a reta y e o 3º lado sobre a reta s

O vértice superior do triângulo tem que ser ponto de encontro da reta y = -x com a reta s

Talvez a questão devesse ser mais precisa, porque relendo, fica meio estranho. Ela não especifica se é uma nova reta que cria o triângulo ou se é a primeira reta dada mesmo. Eu pelo menos fiquei na dúvida agora. Pela minha interpretação, fica assim:

A reta que faz um triângulo com as retas y=x e y=-x não é a reta r: x-2y+3=0, é uma outra reta s que apenas possui mesmo coeficiente angular que ela, por isso não há necessidade de colocar r no desenho. 

A reta s é a reta vermelha, que passa pela reta y=x(verde) e y=-x(azul). Eu devia ter especificado cada uma.

Caso a minha interpretação esteja errada, então o problema quer uma reta paralela a r:x-2y+3=0, onde essa reta r cria um triângulo. Mas se fosse assim, então não precisaríamos saber nada sobre triângulos e outras retas e áreas, porque para ser paralela a uma outra reta, basta que ela tenha o mesmo coeficiente angular que a outra, e como já sabemos que este é 1/2, a nova reta seria s: x-2y+k=0, onde k pode ser qualquer real, e não bate com o gabarito. Por isso eu acho que a primeira interpretação é a certa.

Enunciado:

A equação de uma reta que é paralela à reta x-2y+3=0 e que determina com as retas x-y=0 e x+y=0 um triângulo de área igual a 12 é:


Leia, sem a parte em vermelho:

Quem forma o triângulo não é a reta dada x - 2.y + 3 = 0
Quem forma o triângulo é a reta paralela à reta dada, cuja equação queremos determinar.

Além disso, os lados do triângulo estão sobre a reta y = 0 (amarela), x + y = 0 (verde) e 
y = (1/2).x + k (vermelha)

Sim, foi essa interpretação que eu tive, mas e a reta y=-x?. Continuo sem entender o  porquê de o triângulo ter um lado sobre a reta y=0 quando o enunciado diz que o triângulo é formado pelo cruzamento de x+y=0, x-y=0 e a nova reta.

Desculpe-me eu tinha lido errado reta y = 0 (na realidade é x - y = 0).

Com isto o meu desenho e minha solução estão errados. Vou refazer:



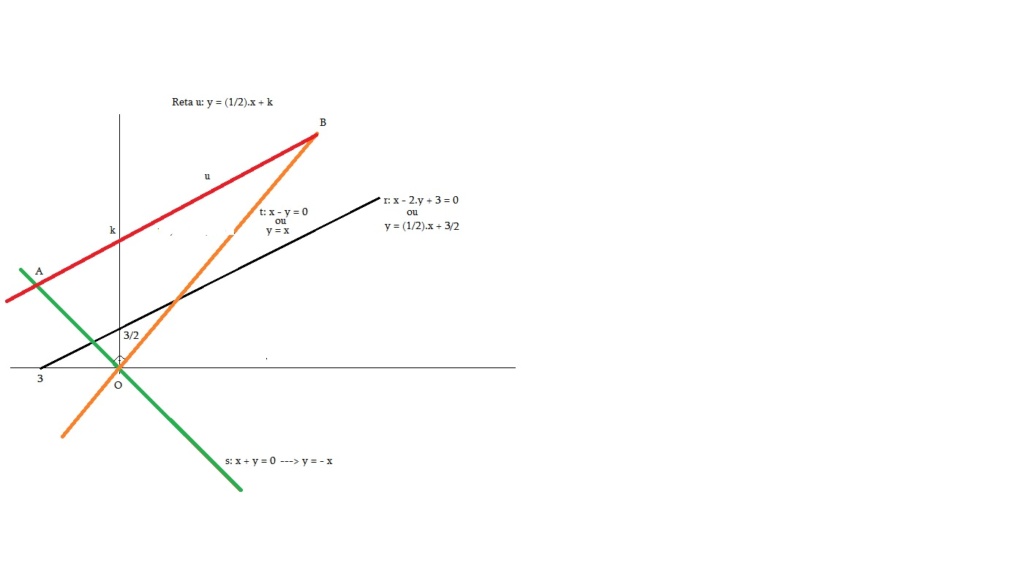
O triângulo de área 12 é OAB ---> O(0, 0) ---> vamos calcular as coordenadas de A e B:

A é o ponto de encontro da reta u: y = (1/2).x + k com a reta s: y = - x

(1/2).xA + k = - x ---> (3/2).xA = - k ---> xA = - (2/3).k ---> yA = (2/3).k

B é o ponto de encontro da reta u: y = (1/2).x + k com a reta t: y = x

(1/2).xB + k = x ---> (1/2).xB = k ---> xB = 2.k ---> yB = 2.k

Note que o triângulo OAB é retângulo em O ---> OA e OB são catetos:

OA² = xA² + yA² ---> OA² = [- (2/3).k]² + [(2/3)k]² ---> OA = (2.√2/3).k

OB² = xB² + yB² ---> OB² = (2.k)² + (2.k)² ---> OB² = 8.k² ---> OB = 2.√2.k

S = OA.OB/2 ---> 12 = [(2.√2/3).k].[2.√2.k]/2 ---> 12 = 4.k/3 ---> k = ±3

Equação da reta u, para k = 3 ---> y = (1/2).x + k ---> y = (1/2).x + 3 ---> x - 2.y + 6 = 0

Equação da reta u, para k = -3 ---> y = (1/2).x + k ---> y = (1/2).x - 3 ---> x - 2.y - 6 = 0


Isto significa que a reta u corta o eixo y em (0, -3), o oposto da minha pressuposição.

Aaaah, agora entendi como fazer. Eu não estava usando o 'k' e acabava cheio de incógnitas. Obrigado pela atenção mestre.
Vi agora que também deve haver outra reta que forma um triângulo de mesma área não é? Só que ela ficaria mais abaixo.

Sim, existem duas soluções: 

1) Reta vermelha na posição da figura, cruzando o eixo y positivo (acima da reta preta)

2) Outra reta vermelha, cruzando o eixo y negativo (abaixo da reta preta)