Geometria Plana
3 participantes
Página 1 de 1

Oziel- Estrela Dourada

- Mensagens : 1518
Data de inscrição : 26/04/2016
Idade : 26
Localização : São Pedro da Aldeia-RJ
 Re: Geometria Plana
Re: Geometria Plana
____________________________________________
Links úteis:
Regras do fórum |
Como colocar imagens nas mensagens |
Como inserir códigos LaTex nas mensagens |
“A dedicação é a mãe da boa sorte.”

Mateus Meireles- Matador

- Mensagens : 763
Data de inscrição : 14/07/2018
Idade : 28
Localização : Fortaleza/CE
 Re: Geometria Plana
Re: Geometria Plana
Matheus, se tiver uma solução trigonométrica seria interessante que nos mostre.
Não é difícil encontrar pela aplicação da lei dos senos e outros resultados trigonométricos, uma equação trigonométrica para tan x como por exemplo
tan x=tan 40 (2cos 40 -1)/(2cos 40 +1) (1)
O problema é como solucionar isso de forma exata para o ângulo x, como na solução geométrica. Acredito que a solução trigonométrica vai ter que envolver alguma aproximação numérica, pois desconheço uma representação exata para tan 10, cos 10 ou sen 10 graus que possa ser facilmente reconhecida. Mas de repente vc tem a resposta.
Edição posterior: ok, já vi como fazer evitando o resultado numérico... dá pra mostrar que o lado direito da equação (1) é igual a tan 10, ou x=10, mas não é nada óbvio, rsrs
Não é difícil encontrar pela aplicação da lei dos senos e outros resultados trigonométricos, uma equação trigonométrica para tan x como por exemplo
tan x=tan 40 (2cos 40 -1)/(2cos 40 +1) (1)
O problema é como solucionar isso de forma exata para o ângulo x, como na solução geométrica. Acredito que a solução trigonométrica vai ter que envolver alguma aproximação numérica, pois desconheço uma representação exata para tan 10, cos 10 ou sen 10 graus que possa ser facilmente reconhecida. Mas de repente vc tem a resposta.
Edição posterior: ok, já vi como fazer evitando o resultado numérico... dá pra mostrar que o lado direito da equação (1) é igual a tan 10, ou x=10, mas não é nada óbvio, rsrs

adriano100- Iniciante
- Mensagens : 47
Data de inscrição : 17/08/2017
Idade : 66
Localização : Piracicaba, SP, Brasil
 Re: Geometria Plana
Re: Geometria Plana
Olá, Adriano
Mais tarde eu escrevo alguma coisa aqui, estou sem tempo no momento
Abraço.
Mais tarde eu escrevo alguma coisa aqui, estou sem tempo no momento
Abraço.
- Dica:
- Lei dos Senos e Prostaféreses
____________________________________________
Links úteis:
Regras do fórum |
Como colocar imagens nas mensagens |
Como inserir códigos LaTex nas mensagens |
“A dedicação é a mãe da boa sorte.”

Mateus Meireles- Matador

- Mensagens : 763
Data de inscrição : 14/07/2018
Idade : 28
Localização : Fortaleza/CE
 Re: Geometria Plana
Re: Geometria Plana
Voltei,
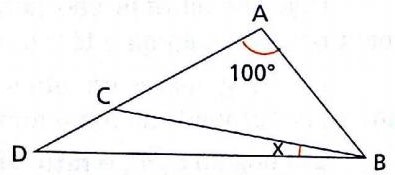
Tome: AC = AB = x, BC = y, CD = y - x
i )
ii)
iii)
Desenvolvendo, temos:
i)







________________________________________________________________________________________________________
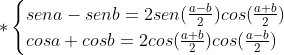
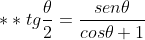
Tome: AC = AB = x, BC = y, CD = y - x
i )
ii)
iii)
Desenvolvendo, temos:
i)
________________________________________________________________________________________________________
____________________________________________
Links úteis:
Regras do fórum |
Como colocar imagens nas mensagens |
Como inserir códigos LaTex nas mensagens |
“A dedicação é a mãe da boa sorte.”

Mateus Meireles- Matador

- Mensagens : 763
Data de inscrição : 14/07/2018
Idade : 28
Localização : Fortaleza/CE
 Re: Geometria Plana
Re: Geometria Plana
Mateus, é isso mesmo, foi onde cheguei depois de pensar um pouco.
Dá pra dar uma simplificada no desenvolvimento inicial, observando no ∆ABC (isósceles), que BC=2b sen 50 (em que b=AC=AB) logo, no ∆DCB, pela lei dos senos, temos
\frac{\text{sen}(40-x)}{BC}=\frac{\text{sen}(x)}{CD}
mas comoBC=AD=2b\, \text{sen}\, 50=2b \cos 40 e CD=BC-b temos
\frac{\text{sen}(40-x)}{2b \cos 40}=\frac{\text{sen}(x)}{2b \cos 40-b}\Leftrightarrow \frac{\text{sen}(40-x)}{2 \cos 40}=\frac{\text{sen}(x)}{2 \cos 40-1}
Em poucos passos podemos chegar a
\tan x=\tan 40\frac{2 \cos 40-1}{2 \cos 40+1}.
Desse ponto é só partir para o abraço como vc bem mostrou.
Inicialmente fiquei meio encalhado nesse ponto, pensando em uma solução numérica mas depois vi como sair usando passos similares aos que vc usou, para mostrar que a expressão da direita é\tan 10
É bem legal termos as soluções geométrica e trigonométrica para o problema.
Dá pra dar uma simplificada no desenvolvimento inicial, observando no ∆ABC (isósceles), que BC=2b sen 50 (em que b=AC=AB) logo, no ∆DCB, pela lei dos senos, temos
mas como
Em poucos passos podemos chegar a
Desse ponto é só partir para o abraço como vc bem mostrou.
Inicialmente fiquei meio encalhado nesse ponto, pensando em uma solução numérica mas depois vi como sair usando passos similares aos que vc usou, para mostrar que a expressão da direita é
É bem legal termos as soluções geométrica e trigonométrica para o problema.
Última edição por adriano100 em Dom 14 Out - 10:50, editado 2 vez(es)

adriano100- Iniciante
- Mensagens : 47
Data de inscrição : 17/08/2017
Idade : 66
Localização : Piracicaba, SP, Brasil
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos