Na figura, ABCD é um retângulo de lados BC = 4 cm e AB

por powermetal Qua 12 Set 2018, 10:44

Na figura, ABCD é um retângulo de lados BC = 4 cm e AB = 6 cm. Os pontos P, Q e R pertencem a uma reta paralela ao lado AD, sendo Q um ponto da diagonal BD. Sabe-se que P e Q são simétricos em relação ao lado AB, e que os pontos Q e R são simétricos em relação ao lado DC.

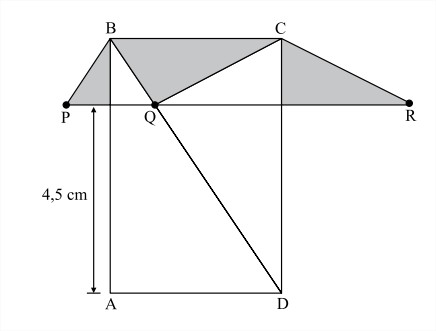
Na figura, ABCD é um retângulo de lados BC = 4 cm e AB Prova_12

Pode-se concluir, então, que a área, em cm², da região sombreada na figura vale:
(A) 6,0.
(B) 5,8.
(C) 5,2.
(D) 4,0.
(E) 3,8.

Resposta A

por adriano100 Qua 12 Set 2018, 11:16

Chame o ponto de cruzamento de AB e PQ de X e o ponto de cruzamento de CD e QR de Y. Note que os triângulos PXB e QXB são congruentes (pela simetria, ângulo 90 e lado comum. Da mesma forma, os triângulos QYC e RYC são congruentes também. Logo a área desejada é exatamente a área do retângulo XBCY com altura AB-4,5 ou 6-4,5 e largura BC=4.

Logo a área desejada é 1,5 x 4 = 6 (resposta A)

por **Elcioschin** Qua 12 Set 2018, 11:28

Sejam M, N os pontos de encontro de AB com PQ e de CD com RQ

AB = CD = 6 ---> AD = BC = MN = 4

Da simetria indicada ---> MP = MQ e NR = NQ

BM = CN = AB - AM ---> BM = CN = 6 - 4,5 ---> BM = CN = 1,5

Triângulos BMQ e BAD são semelhantes: BM/MQ = AB/AD ---> 1,5/MQ = 6/4 ---> MQ = 1 ---> MP = 1

NQ = MN - MQ ---> NQ = 4 - 1 ---> NQ = 3 ---> NR = 3

S = S(BMP) + S(BCQ) + S(CNR)

S = MP.BM/2 + BC.BM/2 + NR.CN/2

S = 1.1,5/2 + 4.1,5/2 + 3.1,5/2

S = 6 cm²