área do triângulo
4 participantes
Página 1 de 1
área do triângulo
por nudwu92 Sáb 21 Abr 2018, 17:49
Considere o triângulo cujos lados estão sobre as retas y = 0, x + 2y = 6 e x – y = 2. Qual é a área do triângulo?
resp: 8/3
nudwu92- Recebeu o sabre de luz
- Mensagens : 195
Data de inscrição : 15/05/2017
Idade : 27
Localização : salvadorr
Re: área do triângulo
por Elcioschin Sáb 21 Abr 2018, 18:08
Determine os vértices do triângulo (pontos de encontro das retas)
S = ∆/2 ---> ∆ é o determinante dos vértices
S = ∆/2 ---> ∆ é o determinante dos vértices
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: área do triângulo
por VctMR Dom 21 Abr 2019, 15:25
Primeiramente, vamos resolver o sistema abaixo:
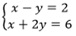
Resolvendo pelo método da substituição, encontramos assim, o vértice A, onde x = 10/3 e y = 4/3.
Do mesmo modo que encontramos o vértice A, vamos encontrar da mesma maneira o B e o C:
B = (2,0) e C (6,0). Logo a base do triângulo será BC = 4, e sua altura em relação ao vértice A = (10/3,4/3), mede 4/3.
-------------------------------
Olá! Como o maluco achou B = (2,0) e C (6,0)? Também não consegui enxergar a base e a altura do triângulo...
Agradeceria a ajuda
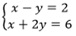
Resolvendo pelo método da substituição, encontramos assim, o vértice A, onde x = 10/3 e y = 4/3.
Do mesmo modo que encontramos o vértice A, vamos encontrar da mesma maneira o B e o C:
B = (2,0) e C (6,0). Logo a base do triângulo será BC = 4, e sua altura em relação ao vértice A = (10/3,4/3), mede 4/3.
-------------------------------
Olá! Como o maluco achou B = (2,0) e C (6,0)? Também não consegui enxergar a base e a altura do triângulo...
Agradeceria a ajuda
VctMR- Jedi
- Mensagens : 255
Data de inscrição : 11/05/2018
Idade : 24
Localização : Brasíla
Re: área do triângulo
por Medeiros Dom 21 Abr 2019, 20:38
conforme enunciado, o terceiro lado do triângulo está sobre a reta suporte y=0, ou seja, o eixo das abscissas. Portanto os pontos B e C estão sobre o eixo x e já sabemos que suas ordenadas são zero.VctMR escreveu:Primeiramente, vamos resolver o sistema abaixo:
Resolvendo pelo método da substituição, encontramos assim, o vértice A, onde x = 10/3 e y = 4/3.
Do mesmo modo que encontramos o vértice A, vamos encontrar da mesma maneira o B e o C:
B = (2,0) e C (6,0). Logo a base do triângulo será BC = 4, e sua altura em relação ao vértice A = (10/3,4/3), mede 4/3.
-------------------------------
Olá! Como o maluco achou B = (2,0) e C (6,0)? Também não consegui enxergar a base e a altura do triângulo...
Agradeceria a ajuda
Faça y=0 nas equações das outras duas retas e obtenha a abscissa dos dois pontos (B e C).
Para vc "enxergar" a base e a altura, sugiro desenhar a situação sobre um par de eixos ordenados.
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Tópicos semelhantes» Area de triangulo
» (F.C.M. STA. CASA - 1981) Área do Triângulo com a Área do círculo
» Area do triangulo
» área do triângulo
» Área triângulo
» (F.C.M. STA. CASA - 1981) Área do Triângulo com a Área do círculo
» Area do triangulo
» área do triângulo
» Área triângulo
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
