Qual a taxa de juros cobrada ao mês?
2 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
 Qual a taxa de juros cobrada ao mês?
Qual a taxa de juros cobrada ao mês?
Uma dívida de $ 3.000,00 será paga em 6 prestações mensais iguais de $ 568,90. Qual a taxa de juros compostos cobrada ao mês?
Luiz 2017- Mestre Jedi

- Mensagens : 693
Data de inscrição : 21/05/2017
Idade : 75
Localização : Vitória, ES.
 Re: Qual a taxa de juros cobrada ao mês?
Re: Qual a taxa de juros cobrada ao mês?
Boa noite!
Estava esperando um exercício deste tipo
Antes de começar a resolução vou pontuar alguns itens de forma a não parecer que 'chutei' os valores das taxas, conforme já fui indagado em outras questões similares.
Vamos 'montar' primeiramente a função valor presente:
\\\boxed{V(i)=-PV+PMT\cdot\sum_{k=1}^n\;\left(1+i\right)^-k}
Ao derivar essa função obtemos sua inclinação:
\\\boxed{V'(i)=-PMT\cdot\sum_{k=1}^n\;k\cdot\left(1+i\right)^{-k-1}}
Perceba que a função é negativa para quaisquer valores de i do domínio, portanto, a função V(i) é DECRESCENTE. Isso nos auxilia (e muito) em saber que a função, partindo de um valor positivo e sendo decrescente, cortará o eixo dos x somente UMA VEZ, ou seja, teremos somente uma única raiz.
A reta tangente ao ponto onde i = 0 corta o eixo das abscissas na posição segundo a equação:
\\V(i)-V(i_0)=V'(0)(i-i_0)\\0-V(0)=V'(0)(i-0)\\\boxed{i=-\dfrac{V(0)}{V'(0)}}
Vamos calcular, então, este valor inicial:
\\V(0)=-PV+PMT\cdot\sum_{k=1}^n\;1\\V(0)=-PV+n\cdot PMT
Agora o valor da derivada em i=0:
\\V'(0)=-PMT\cdot\sum_{k=1}^n\;k\cdot 1\\V'(0)=-PMT\cdot\dfrac{(1+n)n}{2}
Então, o valor inicial da taxa:
\\i=-\dfrac{V(0)}{V'(0)}\\\boxed{i=\dfrac{2(n\cdot PMT-PV)}{n\cdot(n+1)\cdot PMT}}
Agora irei montar as funções sem usar o somatório:
\\\boxed{V(i)=-PV+PMT\cdot\left[\dfrac{1-\left(1+i\right)^{-n}}{i}\right]}
Derivada (omiti a derivação e as simplificações, só coloquei o resultado que obtive):
\\\boxed{V'(i)=PMT\cdot\left[\dfrac{1+i\cdot(n+1)-(1+i)^{n+1}}{i^2\cdot(1+i)^{n+1}}\right]}
Com estas duas funções irei utilizar o método de Newton-Raphson para obter a resposta ao problema.
Dados:
PV = $ 3.000,00
n = 6
PMT = $ 568,90
i = ?
Podemos utilizar a função phi(i) do método de Newton-Raphson:
\\\phi\left(i_{k+1}\right)=i_k-\dfrac{V\left(i_k\right)}{V'\left(i_k\right)}
Primeira 'taxa' (sem 'chutes', hein? ):
):
\\i_0=\dfrac{2(n\cdot PMT-PV)}{n\cdot(n+1)\cdot PMT}\\i_0=\dfrac{2(6\cdot 568,90-3\,000)}{6(6+1)\cdot 568,90}\\\boxed{i_0\approx 3,460312\%}
Montando a tabela:
Então, chegamos a uma taxa de 3,818030% a.m.
Espero ter realmente ajudado
Boa noite!
Estava esperando um exercício deste tipo
Antes de começar a resolução vou pontuar alguns itens de forma a não parecer que 'chutei' os valores das taxas, conforme já fui indagado em outras questões similares.
Vamos 'montar' primeiramente a função valor presente:
Ao derivar essa função obtemos sua inclinação:
Perceba que a função é negativa para quaisquer valores de i do domínio, portanto, a função V(i) é DECRESCENTE. Isso nos auxilia (e muito) em saber que a função, partindo de um valor positivo e sendo decrescente, cortará o eixo dos x somente UMA VEZ, ou seja, teremos somente uma única raiz.
A reta tangente ao ponto onde i = 0 corta o eixo das abscissas na posição segundo a equação:
Vamos calcular, então, este valor inicial:
Agora o valor da derivada em i=0:
Então, o valor inicial da taxa:
Agora irei montar as funções sem usar o somatório:
Derivada (omiti a derivação e as simplificações, só coloquei o resultado que obtive):
Com estas duas funções irei utilizar o método de Newton-Raphson para obter a resposta ao problema.
Dados:
PV = $ 3.000,00
n = 6
PMT = $ 568,90
i = ?
Podemos utilizar a função phi(i) do método de Newton-Raphson:
Primeira 'taxa' (sem 'chutes', hein?
Montando a tabela:
| n | i | V(i) | V'(i) | |
| 0 | 3,460312% | 35,369741 | -9.977,587250 | 3,814804% |
| 1 | 3,814804% | 0,316107 | -9.799,920995 | 3,818029% |
| 2 | 3,818029% | 0,000026 | -9.798,322941 | 3,818030% |
| 3 | 3,818030% | 0,000000 | -9.798,322811 | 3,818030% |
Espero ter realmente ajudado
Boa noite!
____________________________________________
"Nós somos o que fazemos repetidamente. Excelência, então, não é um modo de agir, é um hábito." Aristóteles

Baltuilhe- Fera

- Mensagens : 718
Data de inscrição : 23/12/2015
Idade : 48
Localização : Campo Grande, MS, Brasil
 Re: Qual a taxa de juros cobrada ao mês?
Re: Qual a taxa de juros cobrada ao mês?
baltuilhe escreveu:Boa noite!
Estava esperando um exercício deste tipo
Antes de começar a resolução vou pontuar alguns itens de forma a não parecer que 'chutei' os valores das taxas, conforme já fui indagado em outras questões similares.
Vamos 'montar' primeiramente a função valor presente:\\\boxed{V(i)=-PV+PMT\cdot\sum_{k=1}^n\;\left(1+i\right)^-k}
Ao derivar essa função obtemos sua inclinação:\\\boxed{V'(i)=-PMT\cdot\sum_{k=1}^n\;k\cdot\left(1+i\right)^{-k-1}}
Perceba que a função é negativa para quaisquer valores de i do domínio, portanto, a função V(i) é DECRESCENTE. Isso nos auxilia (e muito) em saber que a função, partindo de um valor positivo e sendo decrescente, cortará o eixo dos x somente UMA VEZ, ou seja, teremos somente uma única raiz.
A reta tangente ao ponto onde i = 0 corta o eixo das abscissas na posição segundo a equação:\\V(i)-V(i_0)=V'(0)(i-i_0)\\0-V(0)=V'(0)(i-0)\\\boxed{i=-\dfrac{V(0)}{V'(0)}}
Vamos calcular, então, este valor inicial:\\V(0)=-PV+PMT\cdot\sum_{k=1}^n\;1\\V(0)=-PV+n\cdot PMT
Agora o valor da derivada em i=0:\\V'(0)=-PMT\cdot\sum_{k=1}^n\;k\cdot 1\\V'(0)=-PMT\cdot\dfrac{(1+n)n}{2}
Então, o valor inicial da taxa:\\i=-\dfrac{V(0)}{V'(0)}\\\boxed{i=\dfrac{2(n\cdot PMT-PV)}{n\cdot(n+1)\cdot PMT}}
Agora irei montar as funções sem usar o somatório:\\\boxed{V(i)=-PV+PMT\cdot\left[\dfrac{1-\left(1+i\right)^{-n}}{i}\right]}
Derivada (omiti a derivação e as simplificações, só coloquei o resultado que obtive):\\\boxed{V'(i)=PMT\cdot\left[\dfrac{1+i\cdot(n+1)-(1+i)^{n+1}}{i^2\cdot(1+i)^{n+1}}\right]}
Com estas duas funções irei utilizar o método de Newton-Raphson para obter a resposta ao problema.
Dados:
PV = $ 3.000,00
n = 6
PMT = $ 568,90
i = ?
Podemos utilizar a função phi(i) do método de Newton-Raphson:\\\phi\left(i_{k+1}\right)=i_k-\dfrac{V\left(i_k\right)}{V'\left(i_k\right)}
Primeira 'taxa' (sem 'chutes', hein?):
\\i_0=\dfrac{2(n\cdot PMT-PV)}{n\cdot(n+1)\cdot PMT}\\i_0=\dfrac{2(6\cdot 568,90-3\,000)}{6(6+1)\cdot 568,90}\\\boxed{i_0\approx 3,460312\%}
Seu critério para obter o valor inicial aproximado de "i" é louvável, MAS, é trabalhoso, quase um tratado sobre matemática ...
Este é mais simples e dá o mesmo resultado:
O resultado final está correto.
Luiz 2017- Mestre Jedi

- Mensagens : 693
Data de inscrição : 21/05/2017
Idade : 75
Localização : Vitória, ES.
 Re: Qual a taxa de juros cobrada ao mês?
Re: Qual a taxa de juros cobrada ao mês?
Luiz 2017 escreveu:baltuilhe escreveu:Boa noite!
Estava esperando um exercício deste tipo
Antes de começar a resolução vou pontuar alguns itens de forma a não parecer que 'chutei' os valores das taxas, conforme já fui indagado em outras questões similares.
Vamos 'montar' primeiramente a função valor presente:\\\boxed{V(i)=-PV+PMT\cdot\sum_{k=1}^n\;\left(1+i\right)^-k}
Ao derivar essa função obtemos sua inclinação:\\\boxed{V'(i)=-PMT\cdot\sum_{k=1}^n\;k\cdot\left(1+i\right)^{-k-1}}
Perceba que a função é negativa para quaisquer valores de i do domínio, portanto, a função V(i) é DECRESCENTE. Isso nos auxilia (e muito) em saber que a função, partindo de um valor positivo e sendo decrescente, cortará o eixo dos x somente UMA VEZ, ou seja, teremos somente uma única raiz.
A reta tangente ao ponto onde i = 0 corta o eixo das abscissas na posição segundo a equação:\\V(i)-V(i_0)=V'(0)(i-i_0)\\0-V(0)=V'(0)(i-0)\\\boxed{i=-\dfrac{V(0)}{V'(0)}}
Vamos calcular, então, este valor inicial:\\V(0)=-PV+PMT\cdot\sum_{k=1}^n\;1\\V(0)=-PV+n\cdot PMT
Agora o valor da derivada em i=0:\\V'(0)=-PMT\cdot\sum_{k=1}^n\;k\cdot 1\\V'(0)=-PMT\cdot\dfrac{(1+n)n}{2}
Então, o valor inicial da taxa:\\i=-\dfrac{V(0)}{V'(0)}\\\boxed{i=\dfrac{2(n\cdot PMT-PV)}{n\cdot(n+1)\cdot PMT}}
Agora irei montar as funções sem usar o somatório:\\\boxed{V(i)=-PV+PMT\cdot\left[\dfrac{1-\left(1+i\right)^{-n}}{i}\right]}
Derivada (omiti a derivação e as simplificações, só coloquei o resultado que obtive):\\\boxed{V'(i)=PMT\cdot\left[\dfrac{1+i\cdot(n+1)-(1+i)^{n+1}}{i^2\cdot(1+i)^{n+1}}\right]}
Com estas duas funções irei utilizar o método de Newton-Raphson para obter a resposta ao problema.
Dados:
PV = $ 3.000,00
n = 6
PMT = $ 568,90
i = ?
Podemos utilizar a função phi(i) do método de Newton-Raphson:\\\phi\left(i_{k+1}\right)=i_k-\dfrac{V\left(i_k\right)}{V'\left(i_k\right)}
Primeira 'taxa' (sem 'chutes', hein?):
\\i_0=\dfrac{2(n\cdot PMT-PV)}{n\cdot(n+1)\cdot PMT}\\i_0=\dfrac{2(6\cdot 568,90-3\,000)}{6(6+1)\cdot 568,90}\\\boxed{i_0\approx 3,460312\%}
Seu critério para obter o valor inicial aproximado de "i" é louvável, MAS, é trabalhoso, quase um tratado sobre matemática ...
Este é mais simples e dá o mesmo resultado:i_0 = \frac{PMT}{PV} - \frac{PV}{PMT \cdot n^2} i_0 = \frac{568,90}{3000} - \frac{3000}{568,90 \cdot 6^2} i_0 = 0,043151819 \boxed{ i_0 \approx 4,31\% }
O resultado final está correto.
Boa noite!
Bom, mesmo resultado não deu, claro, são metodologias diferentes. Veja que comecei por 3,46%, aproximadamente, pela estimativa inicial e cheguei rapidamente na resposta 3,81%.
Sua metodologia também encontra um valor interessante para o início, mas por excesso, né? 4,31%, diferente do meu valor inicial arbirtrado.
Tive que 'discorrer' com esse tratado de matemática, conforme disse, para ver que podemos, sim, arbitrar valores iniciais para as equações deste tipo sem preocupar em
alcançar outras raízes, sendo que elas não existirão. A metodologia nos faz não 'chutar' inicialmente, mas chutar é mais simples e rápido, concorda?
Claro, também sempre observo que nos lembra que sendo uma equação polinomial de grau 6 teria 6 raízes... mas nesse caso não terá, asseguradamente
Espero podermos continuar com essa troca de ideias que considero ótima!
____________________________________________
"Nós somos o que fazemos repetidamente. Excelência, então, não é um modo de agir, é um hábito." Aristóteles

Baltuilhe- Fera

- Mensagens : 718
Data de inscrição : 23/12/2015
Idade : 48
Localização : Campo Grande, MS, Brasil
 Re: Qual a taxa de juros cobrada ao mês?
Re: Qual a taxa de juros cobrada ao mês?
baltuilhe escreveu:Luiz 2017 escreveu:
Seu critério para obter o valor inicial aproximado de "i" é louvável, MAS, é trabalhoso, quase um tratado sobre matemática ...
Este é mais simples e dá o mesmo resultado:i_0 = \frac{PMT}{PV} - \frac{PV}{PMT \cdot n^2} i_0 = \frac{568,90}{3000} - \frac{3000}{568,90 \cdot 6^2} i_0 = 0,043151819 \boxed{ i_0 \approx 4,31\% }
O resultado final está correto.
Boa noite!
Bom, mesmo resultado não deu, claro, são metodologias diferentes. Veja que comecei por 3,46%, aproximadamente, pela estimativa inicial e cheguei rapidamente na resposta 3,81%.
Sua metodologia também encontra um valor interessante para o início, mas por excesso, né? 4,31%, diferente do meu valor inicial arbitrado.
Tive que 'discorrer' com esse tratado de matemática, conforme disse, para ver que podemos, sim, arbitrar valores iniciais para as equações deste tipo sem preocupar em alcançar outras raízes, sendo que elas não existirão. A metodologia nos faz não 'chutar' inicialmente, mas chutar é mais simples e rápido, concorda?
Claro, também sempre observo que nos lembra que sendo uma equação polinomial de grau 6 teria 6 raízes... mas nesse caso não terá, asseguradamente
Espero podermos continuar com essa troca de ideias que considero ótima!
"Boa noite!
Bom, mesmo resultado não deu, claro, são metodologias diferentes."
Você está confundindo valor inicial de "i" para o método de Newton com resultado final. É óbvio que deu o mesmo resultado final de 3,82%. Eu usei o valor inicial de 4,31% e cheguei ao resultado final de 3,82% após 2 ou 3 iterações.
"Sua metodologia também encontra um valor interessante para o início, mas por excesso, né? 4,31%, diferente do meu valor inicial arbitrado."
Como sabe que é por excesso antes de resolver? E que diferença faz se for por excesso ou por falta? O fundamento do método de Newton é que o valor inicial seja "próximo", não importando se mais ou menos.
"Tive que 'discorrer' com esse tratado de matemática, conforme disse, para ver que podemos, sim, arbitrar valores iniciais para as equações deste tipo sem preocupar em alcançar outras raízes, sendo que elas não existirão."
Isto já dito aqui em outras ocasiões: os métodos iterativos encontram uma única raiz, mesmo que a equação admita mais de uma, como é o presente caso, sendo que o processo convergirá para a raiz que estiver mais próxima do valor arbitrado, seja por excesso ou falta, mas sempre o mais próximo. Assim, a escolha do valor inicial é crucial, pois uma má escolha do valor inicial poderá ter como consequência o encontro de uma raiz diferente da procurada. No caso de múltiplas raízes, apenas uma delas será a taxa, as outras não. Felizmente, no presente caso (juros), há muitas maneiras de se determinar um valor inicial apropriado.
"A metodologia nos faz não 'chutar' inicialmente, mas chutar é mais simples e rápido, concorda?"
Não concordo. Sem usar nenhum artifício, nenhum aplicativo, apenas no "chute", que valor inicial você daria para "x", pelo método de Newton, por exemplo, para a seguinte equação:
x12 - 9500x9 + 4750x + 235461969100000 = 0 ?
Será que o chute é mais simples e mais rápido neste caso?
"Claro, também sempre observo que nos lembra que sendo uma equação polinomial de grau 6 teria 6 raízes... mas nesse caso não terá, asseguradamente."
Negativo. Terá sim 7 raízes (o valor presente admite "n+1" raízes). Veja elas:
Como disse anteriormente, das múltiplas raízes apenas uma delas será a taxa, as outras não. Descartando as complexas, as nulas e as negativas, no presente caso tem-se:
Se você tivesse, no "chute", adotado i0=0,0001, por certo o processo teria convergido para a raiz mais próxima que é i=0%, que não é a taxa procurada. Seria um resultado errôneo.
"Espero podermos continuar com essa troca de ideias que considero ótima!"
Eu também.
Sds.
Luiz 2017- Mestre Jedi

- Mensagens : 693
Data de inscrição : 21/05/2017
Idade : 75
Localização : Vitória, ES.
 Re: Qual a taxa de juros cobrada ao mês?
Re: Qual a taxa de juros cobrada ao mês?
Luiz,
Ter raízes no conjunto dos complexos não nos ajuda em nada, concorda?
E, para a equação que te passei, no domínio correto, há somente uma única resposta, asseguradamente, sim, conforme mostrei na derivada, que é negativa para quaisquer valores de i>=0, ou seja, a função é estritamente decrescente, não irá 'cortar' o eixo das abscissas mais do que uma vez.
Veja no gráfico que irei postar.
Abraços!
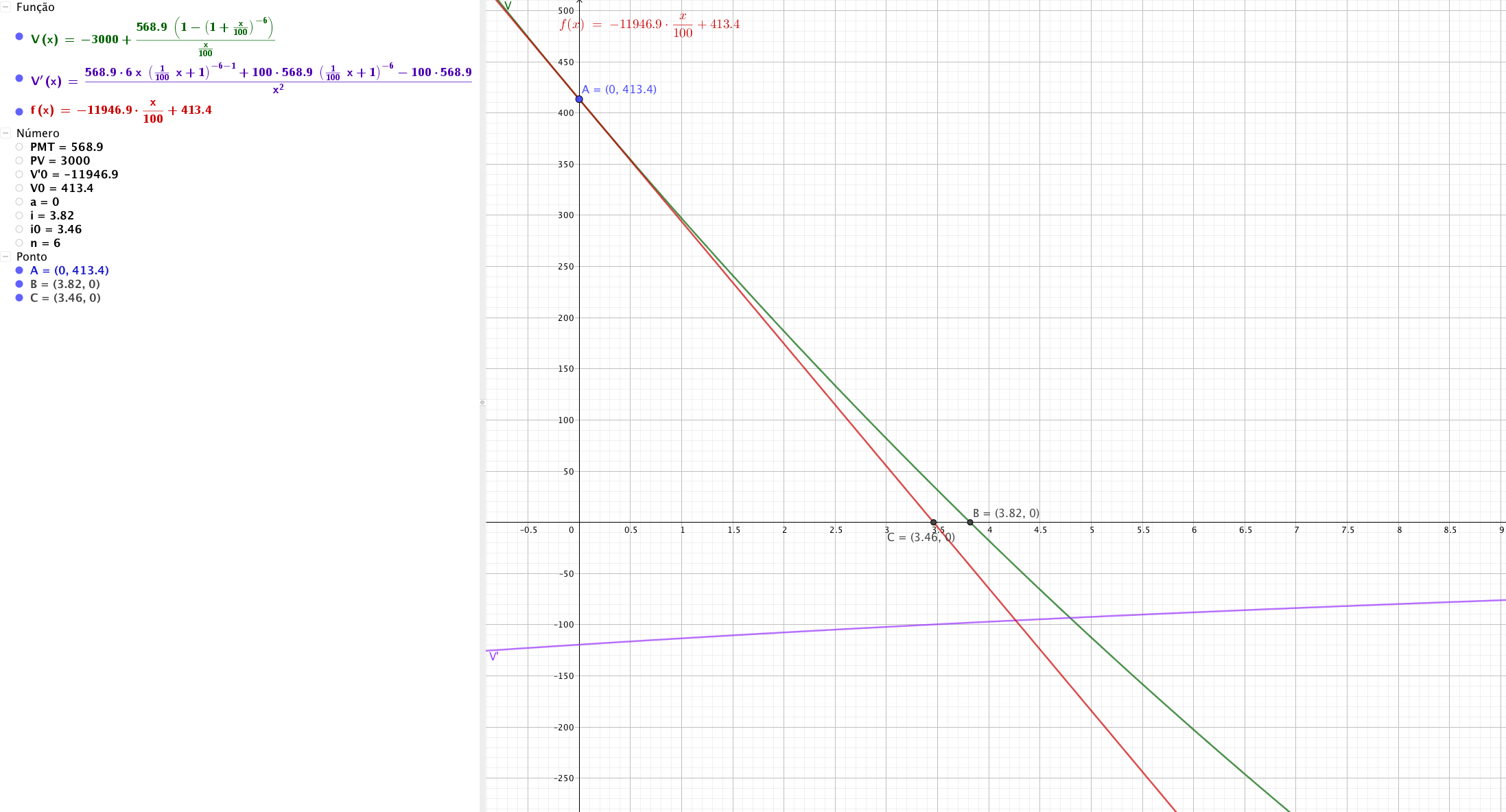
Ter raízes no conjunto dos complexos não nos ajuda em nada, concorda?
E, para a equação que te passei, no domínio correto, há somente uma única resposta, asseguradamente, sim, conforme mostrei na derivada, que é negativa para quaisquer valores de i>=0, ou seja, a função é estritamente decrescente, não irá 'cortar' o eixo das abscissas mais do que uma vez.
Veja no gráfico que irei postar.
Abraços!

____________________________________________
"Nós somos o que fazemos repetidamente. Excelência, então, não é um modo de agir, é um hábito." Aristóteles

Baltuilhe- Fera

- Mensagens : 718
Data de inscrição : 23/12/2015
Idade : 48
Localização : Campo Grande, MS, Brasil
 Re: Qual a taxa de juros cobrada ao mês?
Re: Qual a taxa de juros cobrada ao mês?
Baituilhe.
E, por exemplo, para a seguinte equação:
x12 - 9500x9 + 4750x + 235461969100000 = 0.
Sem usar nenhum artifício, nenhum aplicativo, apenas no "chute", que valor inicial você daria para "x", para solucioná-la pelo método de Newton?
Luiz 2017- Mestre Jedi

- Mensagens : 693
Data de inscrição : 21/05/2017
Idade : 75
Localização : Vitória, ES.
 Re: Qual a taxa de juros cobrada ao mês?
Re: Qual a taxa de juros cobrada ao mês?
Luiz 2017 escreveu:
Baituilhe.
E, por exemplo, para a seguinte equação:
x12 - 9500x9 + 4750x + 235461969100000 = 0.
Sem usar nenhum artifício, nenhum aplicativo, apenas no "chute", que valor inicial você daria para "x", para solucioná-la pelo método de Newton?
Luiz,
Está misturando alhos com bugalhos. Temos aqui neste exercício claramente um problema de matemática financeira, cuja equação é de um tipo específico, e, neste caso, o 'chute' inicial facilmente irá conseguir chegar numa resposta.
Não estou justificando que em TODOS os casos (todas as equações polinomiais), um chute poderia resolver.
Mas, nesta em específico (só pra não perder o costume em resolver), eu 'chutaria' o seguinte valor inicial:
Usando Newton-Raphson:
| n | x | f(x) | f'(x) | |
| 0 | 15,763769 | -100.112.976.213.244,000000 | -146.778.894.670.194,000000 | 15,081703 |
| 1 | 15,081703 | -9.562.702.036.953,120000 | -118.671.310.943.030,000000 | 15,001121 |
| 2 | 15,001121 | -132.929.265.524,250000 | -115.375.765.319.197,000000 | 14,999969 |
| 3 | 14,999969 | -27.048.238,218750 | -115.328.813.197.677,000000 | 14,999969 |
| 4 | 14,999969 | -1,281250 | -115.328.803.640.555,000000 | 14,999969 |
| 5 | 14,999969 | 0,000000 | -115.328.803.640.555,000000 | 14,999969 |
Abraços!
____________________________________________
"Nós somos o que fazemos repetidamente. Excelência, então, não é um modo de agir, é um hábito." Aristóteles

Baltuilhe- Fera

- Mensagens : 718
Data de inscrição : 23/12/2015
Idade : 48
Localização : Campo Grande, MS, Brasil
 Re: Qual a taxa de juros cobrada ao mês?
Re: Qual a taxa de juros cobrada ao mês?
baltuilhe escreveu:Luiz 2017 escreveu:
Baituilhe.
E, por exemplo, para a seguinte equação:
x12 - 9500x9 + 4750x + 235461969100000 = 0.
Sem usar nenhum artifício, nenhum aplicativo, apenas no "chute", que valor inicial você daria para "x", para solucioná-la pelo método de Newton?
Luiz,
Está misturando alhos com bugalhos. Temos aqui neste exercício claramente um problema de matemática financeira, cuja equação é de um tipo específico, e, neste caso, o 'chute' inicial facilmente irá conseguir chegar numa resposta.
Não estou justificando que em TODOS os casos (todas as equações polinomiais), um chute poderia resolver.
Mas, nesta em específico (só pra não perder o costume em resolver), eu 'chutaria' o seguinte valor inicial:\\\sqrt[12]{235461969100000}\approx 15,76
Usando Newton-Raphson:Resolve, né?
n x f(x) f'(x) \phi(x) 0 15,763769 -100.112.976.213.244,000000 -146.778.894.670.194,000000 15,081703 1 15,081703 -9.562.702.036.953,120000 -118.671.310.943.030,000000 15,001121 2 15,001121 -132.929.265.524,250000 -115.375.765.319.197,000000 14,999969 3 14,999969 -27.048.238,218750 -115.328.813.197.677,000000 14,999969 4 14,999969 -1,281250 -115.328.803.640.555,000000 14,999969 5 14,999969 0,000000 -115.328.803.640.555,000000 14,999969
Abraços!
Baltuilhe.
Não estou misturando coisas, e nem promovendo desafios. Estou sim, querendo conhecer o critério que você utiliza para determinar o valor inicial. Este acima por exemplo, do (termo independente)^(1/n), onde n é o grau da equação, eu não conhecia. Dê mais detalhes...
Luiz 2017- Mestre Jedi

- Mensagens : 693
Data de inscrição : 21/05/2017
Idade : 75
Localização : Vitória, ES.
 Re: Qual a taxa de juros cobrada ao mês?
Re: Qual a taxa de juros cobrada ao mês?
baltuilhe escreveu:
Mas, nesta em específico (só pra não perder o costume em resolver), eu 'chutaria' o seguinte valor inicial:\\\sqrt[12]{235461969100000}\approx 15,76
Usando Newton-Raphson:Resolve, né?
n x f(x) f'(x) \phi(x) 0 15,763769 -100.112.976.213.244,000000 -146.778.894.670.194,000000 15,081703 1 15,081703 -9.562.702.036.953,120000 -118.671.310.943.030,000000 15,001121 2 15,001121 -132.929.265.524,250000 -115.375.765.319.197,000000 14,999969 3 14,999969 -27.048.238,218750 -115.328.813.197.677,000000 14,999969 4 14,999969 -1,281250 -115.328.803.640.555,000000 14,999969 5 14,999969 0,000000 -115.328.803.640.555,000000 14,999969
Abraços!
Mas se você colocar como valor inicial:
Pelo método de Newton encontrará como resultado final:
As dez raízes demais são complexas.
Luiz 2017- Mestre Jedi

- Mensagens : 693
Data de inscrição : 21/05/2017
Idade : 75
Localização : Vitória, ES.
Página 1 de 2 • 1, 2 
 Tópicos semelhantes
Tópicos semelhantes» Qual a taxa de juros efetiva cobrada?
» Juros compostos - taxa cobrada
» Calcular a taxa de juros cobrada.
» Qual a taxa cobrada pelo banco?
» Qual a taxa mensal cobrada no financiamento?
» Juros compostos - taxa cobrada
» Calcular a taxa de juros cobrada.
» Qual a taxa cobrada pelo banco?
» Qual a taxa mensal cobrada no financiamento?
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












