1º Maratona de física (ITA,IME,AFA)
+4
Willian Honorio
Faxineiro do ITA
João Soares
nivlek
8 participantes
PiR2 :: Física :: Mecânica Geral
Página 2 de 3
Página 2 de 3 •  1, 2, 3
1, 2, 3 
 1º Maratona de física (ITA,IME,AFA)
1º Maratona de física (ITA,IME,AFA)
Relembrando a primeira mensagem :
Clique no retângulo abaixo e leia seu conteúdo para participar:
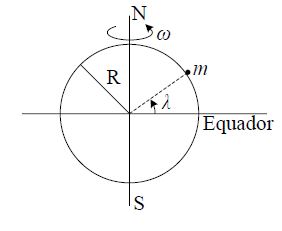
(ITA-10) Considere a Terra como uma esfera homogênea de raio R que gira com velocidade angular uniforme ω em torno do seu próprio eixo Norte-Sul. Na hipótese de ausência de rotação da Terra, sabe-se que a aceleração da gravidade seria dada por g = GM/R². Como ω ≠ 0, um corpo em repouso na superfície da Terra na realidade fica sujeito forçosamente a um peso aparente, que pode ser medido, por exemplo, por um dinamômetro, cuja direção pode não passar pelo centro do planeta. Então, o peso aparente de um corpo de massa m em repouso na superfície da Terra a uma latitude λ é dado por:
A. ( ) mg − mω²Rcos λ.
B. ( ) mg − mω²Rsen2 λ.
C. ( ) mg √1− [2ω²R / g + (ω²R / g)² ] sen²λ.
D. ( )mg √1− [2ω²R / g − (ω²R / g)² ] cos² λ.
E. ( ) mg √1− [2ω²R / g − (ω²R / g)² ] sen²λ.
Resolução:
Sabemos que um corpo situado num astro com aceleração angular w qualquer, está submetido à aceleração gravitacional e à aceleração centrípeta. A composição vetorial dessas duas acelerações nos dará a aceleração aparente, e o produto dessa aceleração pela sua massa nos dará o peso aparente. Tomemos para a resolução o referencial inercial do corpo de massa m. Nesse referencial, agirão seu peso que aponta para o centro geométrico da esfera e à força centrífuga:

O peso aparente é a soma vetorial da força centrífuga com o peso, e sabendo que do triângulo retângulo da figura r=R.cosx:
e que o vetor força centrifuga é o vetor oposto ao força centrípeta:
![\vec{P_{AP}}=\vec{F_{CF}}+\vec{P}\\\\P_{AP}^{2}={F_{CF}}^{2}+P^{2}+2.F_{CF}.P.\cos (180-\lambda )\\P_{AP}^{2}=m^{2}(\omega ^{2}.R.\cos \lambda )^{2}+m^{2}.g^{2}+2.m.\omega ^{2}.R.\cos \lambda .m.g(-cos\lambda )\\\\P_{AP}^{2}=m^{2}.\omega ^{4}.R^{2}.\cos ^{2}\lambda +m^{2}.g^{2}-2m^{2}.\omega ^{2}.R.\cos ^{2}\lambda \\\\P_{AP}^{2}=m^{2}.g^{2}.\left [1+\frac{\omega ^{4}.R^{2}.\cos ^{2}\lambda }{g^{2}}-\frac{2\omega ^{2}.R.\cos ^{2}\lambda }{g} \right ]\\\text{colocando fatores comuns em evidencia, acha-se:}\\\\\boxed{P_{AP}=m.g.\sqrt{1-\left [\frac{2.\omega ^{2}.R}{g}-\left (\frac{\omega ^{2}.R}{g} \right )^{2} \right ].\cos ^{2}\lambda }}](https://latex.codecogs.com/gif.latex?\vec{P_{AP}}=\vec{F_{CF}}+\vec{P}\\\\P_{AP}^{2}={F_{CF}}^{2}+P^{2}+2.F_{CF}.P.\cos&space;(180-\lambda&space;)\\P_{AP}^{2}=m^{2}(\omega&space;^{2}.R.\cos&space;\lambda&space;)^{2}+m^{2}.g^{2}+2.m.\omega&space;^{2}.R.\cos&space;\lambda&space;.m.g(-cos\lambda&space;)\\\\P_{AP}^{2}=m^{2}.\omega&space;^{4}.R^{2}.\cos&space;^{2}\lambda&space;+m^{2}.g^{2}-2m^{2}.\omega&space;^{2}.R.\cos&space;^{2}\lambda&space;\\\\P_{AP}^{2}=m^{2}.g^{2}.\left&space;[1+\frac{\omega&space;^{4}.R^{2}.\cos&space;^{2}\lambda&space;}{g^{2}}-\frac{2\omega&space;^{2}.R.\cos&space;^{2}\lambda&space;}{g}&space;\right&space;]\\\text{colocando&space;fatores&space;comuns&space;em&space;evidencia,&space;acha-se:}\\\\\boxed{P_{AP}=m.g.\sqrt{1-\left&space;[\frac{2.\omega&space;^{2}.R}{g}-\left&space;(\frac{\omega&space;^{2}.R}{g}&space;\right&space;)^{2}&space;\right&space;].\cos&space;^{2}\lambda&space;}})
Alternativa D
Questão para o próximo membro:
(ITA-2015) Um fio de comprimento L e massa específica linear µ é mantido esticado por uma força F em suas extremidades. Assinale a opção com a expressão do tempo que um pulso demora para percorrê-lo:
A)2LF/μ
B)F/2∏.L.μ
C)L√μ/F
D)L/∏.√ μ/F
E)L/2∏.√μ/F
Gabarito: C
Clique no retângulo abaixo e leia seu conteúdo para participar:
- Regras e orientações:
- O objetivo de criar um bom acervo de questões resolvidas dos principais vestibulares militares aqui no Pir2, seja para leitura dos usuários, para quem almeja uma vaga nessas instituições, para quem quiser aprender, praticar ou compartilhar seus conhecimentos nessa ciência independente de seus objetivos, motivou-me a criar esse tópico como uma pequena espécie de ''maratona'' que seguirá regras de fácil entendimento para quem desejar participar.
Do evento:
O primeiro membro (no caso, eu) postará uma questão e a resolverá, nesse mesmo tópico, outra questão será digitada para que o próximo membro interessado resolva. O último deverá resolver essa questão compartilhada pelo último membro, e no mesmo tópico no qual ele a resolveu, deverá digitar outra questão para que o próximo membro interessado resolva. O próximo resolverá a questão proposta pelo último membro, e na sua mesma mensagem, postará outra questão para que o próximo resolva, e assim sucessivamente.
Regras:
1) Todas as regras já conhecidas do fórum deverão ser seguidas, isto é, das notáveis: Questões devem ser digitadas, se conter imagens essas deverão estar junto com as questões, se possuir gabarito esse deve ser postado etc;
2) Pede-se rigor durante as resoluções, simplesmente por enriquecimento do tópico e daqueles que estiverem participando e (ou) lendo. Busque explicar de maneira satisfatória o seu pensamento, compartilhe também imagens bem elaboradas caso sua resolução necessite de esquemas;
3) Como está no título, apenas questões dos três vestibulares citados serão aceitas; pesquise sua questão antes de postá-la para evitar duplicidade
4)Apesar do tópico estar na seção de mecânica devido a orientações dos moderadores, poderão ser postadas questões de qualquer outro assunto da física, desde mecânica até física moderna;
5) A maratona encerrará quando o tópico atingir um número ''bom'' de questões diversificadas. Não interfira com dúvidas durante o processo. Após o término, mensagens para esses fins serão liberadas.
6) Outras regras poderão ser acrescentadas no decorrer da maratona.
(ITA-10) Considere a Terra como uma esfera homogênea de raio R que gira com velocidade angular uniforme ω em torno do seu próprio eixo Norte-Sul. Na hipótese de ausência de rotação da Terra, sabe-se que a aceleração da gravidade seria dada por g = GM/R². Como ω ≠ 0, um corpo em repouso na superfície da Terra na realidade fica sujeito forçosamente a um peso aparente, que pode ser medido, por exemplo, por um dinamômetro, cuja direção pode não passar pelo centro do planeta. Então, o peso aparente de um corpo de massa m em repouso na superfície da Terra a uma latitude λ é dado por:

A. ( ) mg − mω²Rcos λ.
B. ( ) mg − mω²Rsen2 λ.
C. ( ) mg √1− [2ω²R / g + (ω²R / g)² ] sen²λ.
D. ( )mg √1− [2ω²R / g − (ω²R / g)² ] cos² λ.
E. ( ) mg √1− [2ω²R / g − (ω²R / g)² ] sen²λ.
Resolução:
Sabemos que um corpo situado num astro com aceleração angular w qualquer, está submetido à aceleração gravitacional e à aceleração centrípeta. A composição vetorial dessas duas acelerações nos dará a aceleração aparente, e o produto dessa aceleração pela sua massa nos dará o peso aparente. Tomemos para a resolução o referencial inercial do corpo de massa m. Nesse referencial, agirão seu peso que aponta para o centro geométrico da esfera e à força centrífuga:

O peso aparente é a soma vetorial da força centrífuga com o peso, e sabendo que do triângulo retângulo da figura r=R.cosx:
e que o vetor força centrifuga é o vetor oposto ao força centrípeta:
Alternativa D
Questão para o próximo membro:
(ITA-2015) Um fio de comprimento L e massa específica linear µ é mantido esticado por uma força F em suas extremidades. Assinale a opção com a expressão do tempo que um pulso demora para percorrê-lo:
A)2LF/μ
B)F/2∏.L.μ
C)L√μ/F
D)L/∏.√ μ/F
E)L/2∏.√μ/F
Gabarito: C
Última edição por Willian Honorio em Qui 06 Jul 2017, 00:30, editado 1 vez(es)

Willian Honorio- Matador

- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 27
Localização : São Paulo
 Re: 1º Maratona de física (ITA,IME,AFA)
Re: 1º Maratona de física (ITA,IME,AFA)

Mínima condição de equilíbrio estático:
Momento em relação ao centro de massa da barra:
Forças na vertical:
(ITA) Um pequeno objeto de massa m desliza sem atrito sobre um bloco de massa M com o formato de uma casa (veja figura). A área da base do bloco é S e o ângulo que o plano superior do bloco forma com a horizontal é α. O bloco flutua em um líquido de densidade ρ, permanecendo, por hipótese, na vertical durante todo o experimento. Após o objeto deixar o plano e o bloco voltar à posição de equilíbrio, o decréscimo da altura submersa do bloco é igual a:

A) m sen α/Sρ
B) m cos² α/Sρ
C) m cos α/Sρ
D) m/Sρ
E) (m + M)/Sρ
Gabarito: B

Willian Honorio- Matador

- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 27
Localização : São Paulo
 Re: 1º Maratona de física (ITA,IME,AFA)
Re: 1º Maratona de física (ITA,IME,AFA)

Analisando a primeira situação, o contato entre o bloco m e M terá uma força Normal conforme a imagem acima. (Desconsideramos a Px.sen(a) porque o enunciado supos por hipótese que o bloco se mantêm na posição vertical)
Então, teremos as seguintes equações:
No segundo momento, o bloco M estará em equilíbrio e a força peso será igual ao empuxo.
Queremos H - h, que é o decréscimo da altura.
Isolando H e h em (I) e (II), teremos que:
h = M/(pS)
e
H = (M + m.cos²a)/pS
Logo, H - h é (m.cos²a/pS)
Questão:

(IME) Sobre um trilho sem atrito, uma carga +Q vem deslizando do infinito na velocidade inicial v, aproximando-se
de duas cargas fixas de valor -Q. Sabendo que r << d, pode-se afirmar que:
(A) a carga poderá entrar em oscilação apenas em torno de um ponto próximo à primeira carga fixa,
dependendo do valor de v.
(B) a carga poderá entrar em oscilação apenas em torno de um ponto próximo à segunda carga fixa,
dependendo do valor de v.
(C) a carga poderá entrar em oscilação apenas em torno de um ponto próximo ao ponto médio do
segmento formado pelas duas cargas, dependendo do valor de v.
(D) a carga poderá entrar em oscilação em torno de qualquer ponto, dependendo do valor de v.
(E) a carga passará por perto das duas cargas fixas e prosseguirá indefinidamente pelo trilho.
- GAB:
- E)

renan2014- Jedi

- Mensagens : 211
Data de inscrição : 04/07/2015
Localização : Rio de Janeiro
 Re: 1º Maratona de física (ITA,IME,AFA)
Re: 1º Maratona de física (ITA,IME,AFA)
Como sabemos, o potencial no infinito é nulo, e como a carga possui uma velocidade v, ela está dotada de energia cinética. Suponhamos que ao se aproximar das cargas -q a carga +q entre em oscilação. Em dois determinados pontos dessa reta a velocidade da carga +q será nula, e a energia mecânica do sistema será dada por: (-Q))}{d^{2}}+\frac{k.(+Q)(-Q))}{d'^{2}}) que é negativa. A observação acima é um absurdo, pois sendo a força elétrica conservativa e a inexistência de forças dissipativas no problema, não há conservação da energia mecânica do sistema,com a carga +q no infinito a energia é positiva e quando a carga +q entra em oscilação, por suposição, a energia mecânica é negativa. Portanto, a carga prosseguirá seu percurso retilíneo indefinidamente.
que é negativa. A observação acima é um absurdo, pois sendo a força elétrica conservativa e a inexistência de forças dissipativas no problema, não há conservação da energia mecânica do sistema,com a carga +q no infinito a energia é positiva e quando a carga +q entra em oscilação, por suposição, a energia mecânica é negativa. Portanto, a carga prosseguirá seu percurso retilíneo indefinidamente.
(AFA-2013) Uma pequena esfera de massa m é mantida comprimindo uma mola ideal de constante elástica k de tal forma que sua deformação vale x. Ao ser disparada, essa esfera percorre a superfície horizontal até passar pelo ponto A subindo por uma plano inclinado de 45º e, ao final dele, no ponto B, é lançada atingindo uma altura máxima H e caindo no ponto c, distante 3h de A, conforme a figura abaixo.

Considerando a aceleração da gravidade igual a g e desprezando quaisquer formas de atrito, pode-se afirmar que a deformação x será dada por:
\,\left&space;(&space;\frac{3}{5}.\frac{mgh}{k}&space;\right&space;)^{\frac{1}{2}}\\\\b)2.\frac{h^{2}k}{mg}\\c)\,\,\left&space;(&space;\frac{5}{2k}mgH&space;\right&space;)^{\frac{1}{2}}\\d)\left&space;(&space;3.\frac{H^{2}k}{mg}&space;\right&space;)^{\frac{1}{2}})
R: C
Vamos lá pessoal
(AFA-2013) Uma pequena esfera de massa m é mantida comprimindo uma mola ideal de constante elástica k de tal forma que sua deformação vale x. Ao ser disparada, essa esfera percorre a superfície horizontal até passar pelo ponto A subindo por uma plano inclinado de 45º e, ao final dele, no ponto B, é lançada atingindo uma altura máxima H e caindo no ponto c, distante 3h de A, conforme a figura abaixo.

Considerando a aceleração da gravidade igual a g e desprezando quaisquer formas de atrito, pode-se afirmar que a deformação x será dada por:
R: C
Vamos lá pessoal

Willian Honorio- Matador

- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 27
Localização : São Paulo
 Re: 1º Maratona de física (ITA,IME,AFA)
Re: 1º Maratona de física (ITA,IME,AFA)
Observando a imagem, temos:

Desprezando quaisquer formas de atrito, conservamos a energia mecânica do sistema:
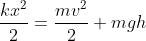 (I)
(I)
Na altura máximo, o corpo possui velocidade vertical nula, logo por Toricelli:
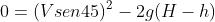 (II)
(II)
Observando o corpo, temos que nos eixos:
Em X: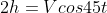
Em Y: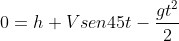 (III)
(III)
Observando as alternativas temos como possibilidade a deformação em função de H ou h, logo necessita que tenhamos uma relação entre H e h para tal. Assim:
Tendo que: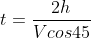 E substituindo em III e relacionando com II acharemos que:
E substituindo em III e relacionando com II acharemos que: 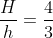
Logo, em função de h: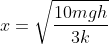
em função de H: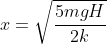
(IME 2018)

As fibras ópticas funcionam pelo Princípio da Reflexão Total, que ocorre quando os raios de luz que seguem determinados percursos dentro da fibra são totalmente refletidos na interface núcleo-casca, permanecendo no interior do núcleo. Considerando apenas a incidência de raios meridionais e que os raios refratados para a casca são perdidos, e ainda, sabendo que os índices de refração do ar, do núcleo e da casca são dados, respectivamente, por n0 , n1 e n2 (n1 > n2 > n0 ), o ângulo máximo de incidência θa , na interface ar-núcleo, para o qual ocorre a reflexão total no interior da fibra é:
Considerações:
• raios meridionais são aqueles que passam pelo centro do núcleo; e
• todas as opções abaixo correspondem a números reais.

Gabarito: C

Desprezando quaisquer formas de atrito, conservamos a energia mecânica do sistema:
Na altura máximo, o corpo possui velocidade vertical nula, logo por Toricelli:
Observando o corpo, temos que nos eixos:
Em X:
Em Y:
Observando as alternativas temos como possibilidade a deformação em função de H ou h, logo necessita que tenhamos uma relação entre H e h para tal. Assim:
Tendo que:
Logo, em função de h:
em função de H:
(IME 2018)

As fibras ópticas funcionam pelo Princípio da Reflexão Total, que ocorre quando os raios de luz que seguem determinados percursos dentro da fibra são totalmente refletidos na interface núcleo-casca, permanecendo no interior do núcleo. Considerando apenas a incidência de raios meridionais e que os raios refratados para a casca são perdidos, e ainda, sabendo que os índices de refração do ar, do núcleo e da casca são dados, respectivamente, por n0 , n1 e n2 (n1 > n2 > n0 ), o ângulo máximo de incidência θa , na interface ar-núcleo, para o qual ocorre a reflexão total no interior da fibra é:
Considerações:
• raios meridionais são aqueles que passam pelo centro do núcleo; e
• todas as opções abaixo correspondem a números reais.

Gabarito: C
Faxineiro do ITA- Recebeu o sabre de luz

- Mensagens : 192
Data de inscrição : 25/04/2017
Idade : 33
Localização : São José Dos Campos
 Re: 1º Maratona de física (ITA,IME,AFA)
Re: 1º Maratona de física (ITA,IME,AFA)

Na primeira face, pela Lei de Snell:
Para ocorrer reflexão total na casca:
Da geometria do Problema, de (eq1) e (eq2):
Próxima questão:
(ITA-2013):Uma pequena bola de massa m é lançada de um ponto P contra uma parede vertical lisa com uma certa velocidade v0, numa direção de ângulo α em relação à horizontal. Considere que apos a colisão a bola retorne ao seu ponto de lançamento, a uma distância d da parede, como mostra a figura. Nestas condições, o coeficiente de restituição deve ser:

a) e=g.d/(vo²sen2 α -g.d)
b)e=2.g.d/(v0².cos2 α -g.d)
c)e=3.g.d/(2.vo².sen2 α -2.g.d)
d)e=4.g.d/(vo²cos2 α -g.d)
e)e=2.g.d/(vo².tg2 α -g.d)
Gabarito: A

Willian Honorio- Matador

- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 27
Localização : São Paulo
 Re: 1º Maratona de física (ITA,IME,AFA)
Re: 1º Maratona de física (ITA,IME,AFA)

O segredo da questão está no fato de que o projétil não tem sua velocidade vertical alterada, pois não há quaisquer forças que vão agir no projétil verticalmente(além da gravitacional).
Logo, por definição a restituição é dada pela seguinte razão entre as velocidades relativas:
No contato com a parede, em função da parede se manter em repouso e que a velocidade vertical não se altera, temos:
Num lançamento oblíquo, sabe-se que ao lançarmos, na altura máxima teremos que a velocidade vertical será nula e assim determinamos o tempo o qual o lançamento irá durar, matematicamente:
E como o tempo de subida é equivalente ao de descida:
Observando o movimento da projétil no eixo x (ANTES DO CHOQUE):
No eixo X, em t, desloca-se d, logo:
E para (DEPOIS DO CHOQUE):
Sabendo que verticalmente a velocidade não se altera, é válido dizer que:
Desenvolvendo chegamos, então: e=g.d/(vo²sen2 α -g.d)
(IME 2018)Duas partículas A e B, carregadas eletricamente com mesmos valores de cargas positivas, partem da origem em velocidade nula no instante t = 0, e têm suas componentes de aceleração em relação aos eixos X e Y regidas pelas seguintes equações temporais:

O instante t min , onde 0 ≤ t min < 2pi, em que a força de repulsão entre as cargas é mínima é:

Gabarito: E
Faxineiro do ITA- Recebeu o sabre de luz

- Mensagens : 192
Data de inscrição : 25/04/2017
Idade : 33
Localização : São José Dos Campos
 Re: 1º Maratona de física (ITA,IME,AFA)
Re: 1º Maratona de física (ITA,IME,AFA)
Resolução da questão proposta pelo IME (utilizarei conceito do Cálculo Integral):
Da Lei de Coulomb:
F=(K.Q.q)/d² ⇒ F ∝ (1/d²)
Para a força eletrostática de repulsão ser mínima, devemos buscar o instante no qual a distância entre as cargas for máxima. Para a partícula A, inicialmente, lembremo-nos que a antiderivada da função velocidade é a aceleração da partícula:
vx(t)= ∫ax(t)dt ⇒ vx(t)=∫cos(t)dt=sen(t)
vy(t)=∫ay(t)dt ⇒ vy(t)=∫sen(t)dt=-cos(t)
Para a partícula B:
vx(t)= ∫ax(t)dt ⇒ vx(t)=∫-cos(t)dt=-∫cos(t)dt=sen(t)
vy(t)=∫ay(t)dt ⇒ vy(t)=∫[sen(t)-cos(t)]dt=∫sen(t)dt-∫cos(t)dt=-cos(t)-sen(t)
Da velocidade relativa entre as partículas nas direções x e y, teremos o sistema batizado C:
C:{vx(t)=sen(t)-[-sen(t)]
vy(t)=-cos(t)-[-sen(t)-cos(t)]
C:{vx(t)=2.sen(t)
vy(t)=sen(t)
A antiderivada da função horária do móvel é a função velocidade, integremos novamente as funções em ambas as direções perpendiculares:
S(t):{Sx(t)=∫2.sen(t)dt=-2.cos(t)
Sy(t)=∫sen(t)dt=-cos(t)
S(t):{Sx(t)=-2.cos(t)
Sy(t)=-cos(t)
Ao adotarmos o referencial em um dos carros, digamos, A, este observa B descrevendo uma trajetória na direção do vetor representante da posição, e como os movimentos são perpendiculares, chamando d a distância entre as partículas:
d²=[-2.cos(t)]²+[-cos(t)]²
d(t)=√5.lcos(t)l
A distância máxima ocorrerá quando l cos(t) l for máximo. Esboçando a função no plano cartesiano, e tomando o intervalo dado na questão 0<=tmín < 2 ∏, é fácil perceber que a resposta será:
Tmín= ∏ s
Próxima questão:
(AFA-2012) A figura abaixo apresenta a configuração de uma onda estacionária que se forma em uma corda inextensível de comprimento L e densidade linear μ quando esta é submetida a oscilações de frequência f0, através de uma fonte presa em uma das extremidades. A corda é tensionada por um corpo homogêneo e maciço de densidade ρ, preso na outra extremidade, que se encontra inicialmente num recipiente vazio.

Considere que o recipiente seja lentamente preenchido com um líquido homogêneo de densidade δ e que, no equilíbrio, o corpo M fique completamente submerso nesse líquido. Dessa forma, a nova configuração de onda estacionária que se estabelece na corda é mostrada na figura 2:

Nessas condições, a razão ρ/δ entre as densidades do corpo e do líquido é:
a) 3/2
b) 4/3
c) 5/4
d) 6/5
Gabarito: B
Da Lei de Coulomb:
F=(K.Q.q)/d² ⇒ F ∝ (1/d²)
Para a força eletrostática de repulsão ser mínima, devemos buscar o instante no qual a distância entre as cargas for máxima. Para a partícula A, inicialmente, lembremo-nos que a antiderivada da função velocidade é a aceleração da partícula:
vx(t)= ∫ax(t)dt ⇒ vx(t)=∫cos(t)dt=sen(t)
vy(t)=∫ay(t)dt ⇒ vy(t)=∫sen(t)dt=-cos(t)
Para a partícula B:
vx(t)= ∫ax(t)dt ⇒ vx(t)=∫-cos(t)dt=-∫cos(t)dt=sen(t)
vy(t)=∫ay(t)dt ⇒ vy(t)=∫[sen(t)-cos(t)]dt=∫sen(t)dt-∫cos(t)dt=-cos(t)-sen(t)
Da velocidade relativa entre as partículas nas direções x e y, teremos o sistema batizado C:
C:{vx(t)=sen(t)-[-sen(t)]
vy(t)=-cos(t)-[-sen(t)-cos(t)]
C:{vx(t)=2.sen(t)
vy(t)=sen(t)
A antiderivada da função horária do móvel é a função velocidade, integremos novamente as funções em ambas as direções perpendiculares:
S(t):{Sx(t)=∫2.sen(t)dt=-2.cos(t)
Sy(t)=∫sen(t)dt=-cos(t)
S(t):{Sx(t)=-2.cos(t)
Sy(t)=-cos(t)
Ao adotarmos o referencial em um dos carros, digamos, A, este observa B descrevendo uma trajetória na direção do vetor representante da posição, e como os movimentos são perpendiculares, chamando d a distância entre as partículas:
d²=[-2.cos(t)]²+[-cos(t)]²
d(t)=√5.lcos(t)l
A distância máxima ocorrerá quando l cos(t) l for máximo. Esboçando a função no plano cartesiano, e tomando o intervalo dado na questão 0<=tmín < 2 ∏, é fácil perceber que a resposta será:
Tmín= ∏ s
Próxima questão:
(AFA-2012) A figura abaixo apresenta a configuração de uma onda estacionária que se forma em uma corda inextensível de comprimento L e densidade linear μ quando esta é submetida a oscilações de frequência f0, através de uma fonte presa em uma das extremidades. A corda é tensionada por um corpo homogêneo e maciço de densidade ρ, preso na outra extremidade, que se encontra inicialmente num recipiente vazio.

Considere que o recipiente seja lentamente preenchido com um líquido homogêneo de densidade δ e que, no equilíbrio, o corpo M fique completamente submerso nesse líquido. Dessa forma, a nova configuração de onda estacionária que se estabelece na corda é mostrada na figura 2:

Nessas condições, a razão ρ/δ entre as densidades do corpo e do líquido é:
a) 3/2
b) 4/3
c) 5/4
d) 6/5
Gabarito: B

Willian Honorio- Matador

- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 27
Localização : São Paulo
 Re: 1º Maratona de física (ITA,IME,AFA)
Re: 1º Maratona de física (ITA,IME,AFA)
Temos que a velocidade de propagação de uma onda na corda vai se dar por:
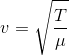
No primeiro caso, a tensão na corda será o peso do bloco:
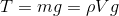
E temos que:
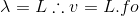
Portanto:
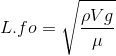
Para o segundo caso, a tensão na corda será a resultante entre peso e empuxo causado pelo líquido:

E temos que:
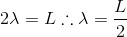
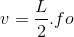
Portanto:
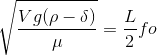
Isolando L.fo em cada um e após isso igualando:

(AFA-2017) Dois pequenos corpos A e B são ligados a uma haste rígida através de fios ideias de comprimentos La e Lb, respectivamente, conforme a figura a seguir.
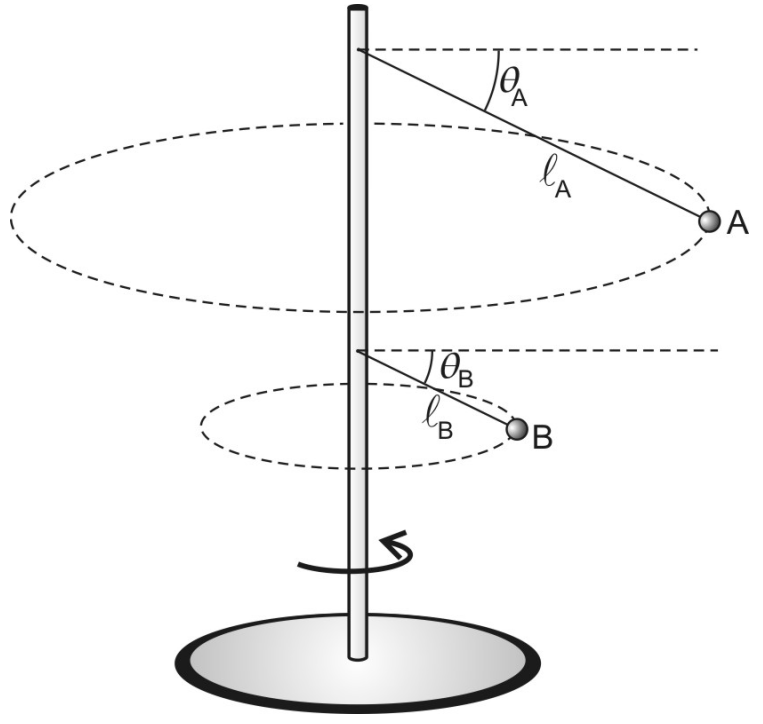
A e B giram em sincronia com a haste, com velocidades escalares constantes Va e Vb, e fazem com a direção horizontal ângulos respectivamente. Considerando La=4Lb, a razão Va/Vb, em função de (teta)a e (teta)b, é igual a
respectivamente. Considerando La=4Lb, a razão Va/Vb, em função de (teta)a e (teta)b, é igual a

gab a)
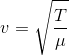
No primeiro caso, a tensão na corda será o peso do bloco:
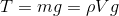
E temos que:
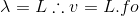
Portanto:
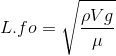
Para o segundo caso, a tensão na corda será a resultante entre peso e empuxo causado pelo líquido:

E temos que:
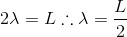
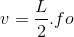
Portanto:
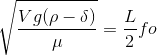
Isolando L.fo em cada um e após isso igualando:

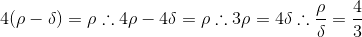
(AFA-2017) Dois pequenos corpos A e B são ligados a uma haste rígida através de fios ideias de comprimentos La e Lb, respectivamente, conforme a figura a seguir.

A e B giram em sincronia com a haste, com velocidades escalares constantes Va e Vb, e fazem com a direção horizontal ângulos
 respectivamente. Considerando La=4Lb, a razão Va/Vb, em função de (teta)a e (teta)b, é igual a
respectivamente. Considerando La=4Lb, a razão Va/Vb, em função de (teta)a e (teta)b, é igual a 
gab a)

RodrigoA.S- Elite Jedi

- Mensagens : 449
Data de inscrição : 12/07/2017
Idade : 24
Localização : Nova Iguaçu
 Re: 1º Maratona de física (ITA,IME,AFA)
Re: 1º Maratona de física (ITA,IME,AFA)
Observando a figura abaixo, teremos o equilíbrio na horizontal e na vertical na esfera A:

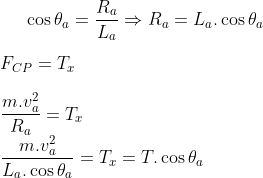
Na vertical:
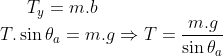
Substituindo o módulo da tração na equação anterior e manipulando:
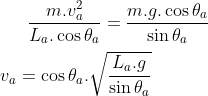
Observando os termos dessa equação, é seguro concluirmos para a esfera B que:

Relacionando esses termos e utilizando a informação dada La=4.Lb:

Alternativa A
(ITA-1990) Uma pequena esfera penetra com velocidade v um tubo oco, recurvado, colocado num plano vertical, como mostrado na figura, num local onde a aceleração da gravidade é g. Supondo que a esfera percorra a região ao tubo sem atrito e acabe saindo horizontalmente pela extremidade, pergunta-se: que distância x, horizontal, ele percorrerá até tocar o solo?

a)})
b)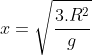
c)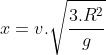
d)})
e) outro valor
Resposta: D

Na vertical:
Substituindo o módulo da tração na equação anterior e manipulando:
Observando os termos dessa equação, é seguro concluirmos para a esfera B que:
Relacionando esses termos e utilizando a informação dada La=4.Lb:
Alternativa A
(ITA-1990) Uma pequena esfera penetra com velocidade v um tubo oco, recurvado, colocado num plano vertical, como mostrado na figura, num local onde a aceleração da gravidade é g. Supondo que a esfera percorra a região ao tubo sem atrito e acabe saindo horizontalmente pela extremidade, pergunta-se: que distância x, horizontal, ele percorrerá até tocar o solo?

a)
b)
c)
d)
e) outro valor
Resposta: D

Willian Honorio- Matador

- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 27
Localização : São Paulo
 Re: 1º Maratona de física (ITA,IME,AFA)
Re: 1º Maratona de física (ITA,IME,AFA)
Vamos lá!
Da conservação da energia temos:
m.v^2 / 2 + m.g.2R = m.v'^2 / 2 + m.g.3R/2
v' = √ v^2 + g.R
O tempo de queda:
3R/2 = g.t^2 /2 --> t = √ 3R/g
Por fim:
x = v' . t
x = √ 3R/g . (v^2 + g.R)
Resolução no papel:

Próxima questão:
(ITA - 2012) - Um gerador elétrico alimenta um circuito cuja resistëncia equivalente varia de 50 a 150Ω, dependendo das condições de uso desse circuito. Lembrando que, com a resistência mínima, a potência útil do gerador é máxima, então, o rendimento do gerador na situação de resistência máxima, é igual a
a) 0,25
b) 0,50
c) 0,67
d) 0,75
e) 0,90
Da conservação da energia temos:
m.v^2 / 2 + m.g.2R = m.v'^2 / 2 + m.g.3R/2
v' = √ v^2 + g.R
O tempo de queda:
3R/2 = g.t^2 /2 --> t = √ 3R/g
Por fim:
x = v' . t
x = √ 3R/g . (v^2 + g.R)
Resolução no papel:

Próxima questão:
(ITA - 2012) - Um gerador elétrico alimenta um circuito cuja resistëncia equivalente varia de 50 a 150Ω, dependendo das condições de uso desse circuito. Lembrando que, com a resistência mínima, a potência útil do gerador é máxima, então, o rendimento do gerador na situação de resistência máxima, é igual a
a) 0,25
b) 0,50
c) 0,67
d) 0,75
e) 0,90
- Gab::
- d

Emanoel Mendonça- Fera

- Mensagens : 1744
Data de inscrição : 23/06/2017
Idade : 26
Localização : Resende, RJ, Brasil
Página 2 de 3 •  1, 2, 3
1, 2, 3 
 Tópicos semelhantes
Tópicos semelhantes» Maratona ITA, IME e AFA
» Maratona - Logaritmo
» Equação (Logaritmo) - Maratona
» Maratona novo ENEM!
» Maratona Cearense de Química
» Maratona - Logaritmo
» Equação (Logaritmo) - Maratona
» Maratona novo ENEM!
» Maratona Cearense de Química
PiR2 :: Física :: Mecânica Geral
Página 2 de 3
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|













