Solução de uma equação... !!!

por **alissonsep** Qua 13 Abr 2011, 23:13

solucione a equação 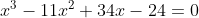$Solução de uma equação... !!! Gif$ , sabendo que a diferença entre duas de suas raízes é 3.

R= { 1,4,6 }

Amigos interpretei assim:

Condição do problema: x1-x2= 3, mas o problema é que não consegui chegar a uma relação de Girard que relacione essa condição !

Agradeço a quem me ajudar

por **Adam Zunoeta** Qua 13 Abr 2011, 23:34

Oi alissonsep, essa é parecida com essa:
https://pir2.forumeiros.com/t12769-raiz-igual-ao-dobro-da-outra-na-equacao

A única diferença é que:

x1+x2+y=11

x1-x2=3 ---->x1=3-x2

Depois so fazer a mesma coisa que no outro exercício.
Caso não consiga só falar , que eu termino pra você xD.

por **alissonsep** Qua 13 Abr 2011, 23:44

Obrigado amigo, mas vou tentar, qualquer dúvida eu falo !

Obrigado

por **alissonsep** Qui 14 Abr 2011, 00:29

Amigo balanar, tentei mas infelizmente não consegui, tentei pegar a outra como modelo mas não deu, peço sua ajuda !

a propósito esse x1-x2=3 ==> x1=3+x2 ou é daquela outra maneira mesmo ?

Obrigado

por **Adam Zunoeta** Qui 14 Abr 2011, 00:43

Vamos lá xD.
Sejam a,b e c as raízes, então das relações de Girard vem:
a+b+c=11--->(1)
ab+ac+bc=34--->(2)

a-b=3--->a=3+b---->(3)

(3) em (1) vem: --->3+b+b+c=11 ---->c=8-2b----->(4)

(3) e (4) em (2) vem:

-3b²+13-10=0
b=1
b=-1
Como saber qual pegar? So testando as raízes =/.
Então:
b=1
a=4
c=8-2=6

por **Adam Zunoeta** Qui 14 Abr 2011, 00:57

Oi alissonsep, você também poderia usar Briot-Ruffini, já que temos uma raíz 1. Então você teria uma equação do segundo grau, que fica mais fácil de trabalhar.

por **alissonsep** Qui 14 Abr 2011, 01:26

e depois Baskara e achei: x'= 6 e x''= 4

logo a solução fica { 1,4,6 }

Como vc falou amigo !

Obrigado ! e a propósito meu procedimento está certo ?

uma dúvida: eu poderia usar essa relação abc=-d/a ? se não, quando posso usa-lá ou melhor quando saberei a hora de usar essa relação no problema ?

Obrigado mais uma vez balanar !

por **Adam Zunoeta** Qui 14 Abr 2011, 01:44

Obrigado ! e a propósito meu procedimento está certo ?
Sim, está.
uma dúvida: eu poderia usar essa relação abc=-d/a ?

Um exemplo com as relações de Girard.
x³+2x²+x+8=0

As relações de Girard dele são:
Sejam a,b,c e d as raízes de x³+2x²+x+8=0.
Então:
a+b+c=-2
ab+ac+bc=1
abc=-8

Sim, poderia.

se não, quando posso usa-lá ou melhor quando saberei a hora de usar essa relação ?

Depende da questão, você tem que tentar achar a relação que seja mais simples pra resolver a equação ou a que de menos conta.

por **alissonsep** Qui 14 Abr 2011, 06:32

amigo, tenho uma pergunta sobre esse método de resolução:

Esse método da sua resolução, de isolar uma incógnita em uma equação e aplicá-la em outra, tem algum nome na matemática ?

tipo, sistema....., algum nome para que possa ser identificado esse procedimento !

E aliás, obrigado, suas dicas e resoluções ajudaram bastante mesmo !

Obrigado amigo

por **Adam Zunoeta** Qui 14 Abr 2011, 08:44

amigo, tenho uma pergunta sobre esse método de resolução:

Esse método da sua resolução, de isolar uma incógnita em uma equação e aplicá-la em outra, tem algum nome na matemática ?
Tem sim , método do balanar rsrsrs, brincadeira tem não.
Eu so usei as relações de Girard e manipulei as equações de forma a obter uma equação simples que forneça a resposta.