HIDRODINÂMICA
PiR2 :: Física :: Mecânica dos Fluidos
Página 1 de 1
 HIDRODINÂMICA
HIDRODINÂMICA
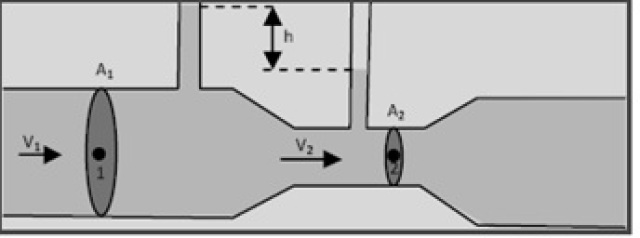
Pretende-se medir a vazão de um líquido que escoa por uma canalização. Para isso, utiliza-se um aparelho chamado tubo de Venturi, que consiste essencialmente de um tubo cujas seções têm áreas A1 e A2 conhecidas. O tubo de Venturi é inserido na canalização, conforme mostra a figura. Sendo A1=10 cm2, A2=5,0 cm2, h=0,60 m, g=10m/s2 e γ=12.103 kg/m3 o peso específico do líquido, determine a vazão (m3/s) do líquido através da canalização.

nicgomess- Iniciante
- Mensagens : 22
Data de inscrição : 17/01/2016
Idade : 25
Localização : Rio de Janeiro,RJ,Brasil
 Re: HIDRODINÂMICA
Re: HIDRODINÂMICA
Equação da continuidade da vazão:
Z1=Z2 -> A1v1=A2v2
Equação de Bernoulli:
p_1 + \frac{\gamma v_1^2}{2} = p_2 + \frac{\gamma v_2^2}{2}
Substituindo o primeiro resultado:
p_1 - p_2 = \frac{\gamma v_1^2}{2}((\frac{A_1}{A_2})^2 - 1)
Uma vez que, pelo Teorema de Stevin,p_1 - p_2 = \gamma g h teremos:
\frac{\gamma v_1^2}{2}((\frac{A_1}{A_2})^2 - 1) = \gamma g h , com \frac{A_1}{A_2}=2
v_1 = \frac{2gh}{3} = \frac{2 \cdot 10 \cdot 0.6}{3} = 2.0\text{m/s}
Logo, Z=A1v1 = 10cm² * 2m/s = 2.0 * 10^(-3) m³/s
Z1=Z2 -> A1v1=A2v2
Equação de Bernoulli:
Substituindo o primeiro resultado:
Uma vez que, pelo Teorema de Stevin,
Logo, Z=A1v1 = 10cm² * 2m/s = 2.0 * 10^(-3) m³/s
Última edição por gabrieldpb em Seg 25 Jan 2016, 19:58, editado 1 vez(es) (Motivo da edição : O valor de A1/A2 estava errado)
Convidado- Convidado
 Re: HIDRODINÂMICA
Re: HIDRODINÂMICA
Obrigada Gabriel!!!!!!!!
nicgomess- Iniciante
- Mensagens : 22
Data de inscrição : 17/01/2016
Idade : 25
Localização : Rio de Janeiro,RJ,Brasil
PiR2 :: Física :: Mecânica dos Fluidos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












