As leis de Newton constituem uma muito sólida base da Dinâmica. Sabemos da segunda lei, também chamada de "fundamental" que uma força aplicada a um corpo que não está fixo produz nele uma aceleração. Matematicamente isso se expressa como
Ora, é claro que os efeitos de uma força só se manifestam enquanto ela atua, só há aceleração se houver uma força, vamos agora frisar: externa ao corpo. Ninguém é capaz de suspender seu próprio corpo puxando-se para cima pelos cabelos.
Isso está expresso na primeira lei, ou lei da Inércia. De acordo com ela um corpo só altera o seu estado de equilíbrio (que pode ser o repouso, ou o movimento retilíneo e uniforme) sob a ação de uma força externa.
Outra coisa que é preciso destacar neste momento é que um corpo newtoniano é representado fisicamente pelo seu centro de massa, isto é, um ponto no qual estaria concentrada toda a sua massa. A aceleração do corpo é a aceleração do seu centro de massa.
Quando uma força atua num corpo durante um certo tempo definimos a grandeza chamada Impulso.
ou, de acordo com a segunda lei,
e da definição de aceleração
O impulso é igual ao produto entre a massa do corpo e a sua variação de velocidade. Isso nos coloca diante de uma grandeza importante representada pelo produto entre massa e velocidade de um corpo. Importante, porque podemos bem ver que, na ausência de uma força externa, essa grandeza tem de ser invariável, obedecendo à primeira lei, já que a massa, nas condições na mecânica de Newton, é uma constante e a velocidade só pode ser alterada mediante a ação de força externa. Definimos assim o momento linear, ou quantidade de movimento de um corpo ao produto:
Sendo portanto o Impulso igual à variação da quantidade de movimento de um corpo.
estamos destacando a notação vetorial para lembrar que, assim como a velocidade, a quantidade de movimento é um vetor e sua invariância, ou conservação, é de natureza vetorial. A quantidade de movimento se conserva em módulo, direção e sentido.
Corpo isolado e sistema de corpos
Suponha um patinador no gelo, inicialmente em repouso, que recebe um impulso e passa a deslizar em linha reta. Já sabemos que esse MRU não pode se alterar e consequentemente a quantidade de movimento do patinador, sem a ação de outra força externa a ele.
Imagine agora uma dupla de patinadores que estão inicialmente em repouso e segurando-se um ao outro. O conjunto então recebe também um impulso e passa a descrever um MRU.
Temos agora dois corpos cujo movimento conjunto estamos avaliando. Dizemos que esse objeto de estudo constitui um sistema de corpos. Do ponto de vista de Newton cada patinador é um corpo isolado e é dinamicamente representado pelo seu centro de massa. O sistema constituído pelos dois patinadores também é um corpo newtoniano representado dinamicamente pelo seu centro de massa. Note também que esse centro de massa do sistema não estará situado no corpo de nenhum dos patinadores, mas será um ponto virtual entre eles.

Em ambos os casos os patinadores podem erguer ou abaixar a perna, ou mover os braços que nada afetará o movimento (trajetória e velocidade) do centro de massa. Rigorosamente o que obedece às leis de Newton é o centro de massa.
Se os patinadores da dupla em dado momento soltarem as mãos continuarão em repouso relativo um ao outro e o centro de massa do sistema constituído por eles permanecerá na mesma posição relativa, descrevendo o mesmo movimento.
- o que acontece se, em vez se se soltarem apenas, os patinadores se empurrarem mutuamente?
Do ponto de vista do patinador à esquerda, ele recebeu uma força (externa em relação a ele) vinda da direita e vai se deslocar para a esquerda. Analogamente o outro patinador deve se deslocar para a direita. Do ponto de vista do sistema constituído por ambos, entretanto, nenhuma força externa atuou. Em relação ao sistema, portanto, prevalece a primeira lei, lei da Inércia, e o centro de massa do sistema deve permanecer no mesmo MRU, sem alteração.
Se as massas dos patinadores forem iguais ambos manterão a mesma distância da trajetória do centro de massa comum.
Nenhuma força surgida internamente ao sistema pode alterar seu estado de movimento retilíneo e uniforme ou seu estado de repouso.
Da mesma maneira podemos pensar em uma granada lançada obliquamente e que explode no ar enquanto descreve o arco de parábola. Após a explosão os diversos fragmentos tomarão velocidades e trajetórias diferentes, porém esses movimentos estarão condicionados de tal maneira que a qualquer instante que calcularmos o centro de massa constituído por eles, este estará descrevendo o mesmo arco de parábola original.

Um
último
exemplo
Esta é uma aplicação clássica que aparece frequentemente em exercícios sobre o assunto.
Um barco de 8m e massa 120 kg repousa sobre as águas serenas de um lago. De pé sobre o barco está uma pessoa de 60 kg posicionada numa das extremidades do barco. Em seguida a pessoa se desloca até a outra extremidade. Como analisar o que ocorre?
1- não há resultante externa atuando. A única força sobre cada um deles é o atrito entre os pés da pessoa e o barco.
2- a força de atrito é a responsável pelo movimento da pessoa e sua reação no barco será responsável por um movimento do barco no sentido oposto.
3- nessa situação a quantidade de movimento do sistema se conserva.
4- o centro de massa do sistema, que estava em repouso, deverá permanecer em repouso.
5- para isso os movimentos relativos entre a pessoa e o barco devem ser de tal forma que o deslocamento de ambos mantenha o centro de massa do sistema no mesmo lugar.
6- sendo suas massas diferentes, suas velocidades e deslocamentos também o serão.
7- Importante: não é intuitivo, mas a primeira lei nos garante que quando a pessoa parar, o barco também vai parar, ou, de outra forma, o centro de massa do sistema se deslocaria.
Impondo a condição da conservação da quantidade de movimento, teremos:
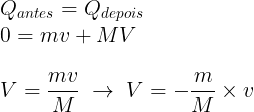
a velocidade de deslocamento do barco será proporcional à relação entre as massas, e portanto, o deslocamento do barco também o será. O sinal negativo indica o sentido oposto.

Esta é uma aplicação clássica que aparece frequentemente em exercícios sobre o assunto.
Um barco de 8m e massa 120 kg repousa sobre as águas serenas de um lago. De pé sobre o barco está uma pessoa de 60 kg posicionada numa das extremidades do barco. Em seguida a pessoa se desloca até a outra extremidade. Como analisar o que ocorre?
1- não há resultante externa atuando. A única força sobre cada um deles é o atrito entre os pés da pessoa e o barco.
2- a força de atrito é a responsável pelo movimento da pessoa e sua reação no barco será responsável por um movimento do barco no sentido oposto.
3- nessa situação a quantidade de movimento do sistema se conserva.
4- o centro de massa do sistema, que estava em repouso, deverá permanecer em repouso.
5- para isso os movimentos relativos entre a pessoa e o barco devem ser de tal forma que o deslocamento de ambos mantenha o centro de massa do sistema no mesmo lugar.
6- sendo suas massas diferentes, suas velocidades e deslocamentos também o serão.
7- Importante: não é intuitivo, mas a primeira lei nos garante que quando a pessoa parar, o barco também vai parar, ou, de outra forma, o centro de massa do sistema se deslocaria.
Impondo a condição da conservação da quantidade de movimento, teremos:
a velocidade de deslocamento do barco será proporcional à relação entre as massas, e portanto, o deslocamento do barco também o será. O sinal negativo indica o sentido oposto.

