Órbitas Geoestacionárias

Órbita Geoestacionária

Órbitas Estáveis

O estudo dos movimentos circulares nos ensinou que uma trajetória circular só pode ser mantida pela ação de uma força de direção radial e voltada para o centro da trajetória denominada '''Força Centrípeta'''. Essa trajetória só será estável se a força centrípeta tiver a intensidade necessária e suficiente para conservá-la. Aprendemos a relação que mantém esse equilíbrio:

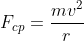$\;F_{cp}=\frac{mv^2}{r}$ ou, em função da velocidade angular 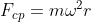$F_{cp}=m\omega^2r$

ou seja, um corpo de massa '''m''', dotado de velocidade tangencial '''v''', ou angular 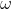$\omega$ , poderá se manter numa trajetória circular de raio '''r''' desde que a força centrípeta conserve a relação descrita. Força menor do que aquela implicará em afastamento e perda da trajetória, força maior implicará em aproximação e perda da trajetória.

Órbitas gravitacionais

A força da gravidade dos planetas e estrelas tem a característica de ser radial e dirigida para o centro da massa que a produz e, portanto pode atuar, e atua, como força centrípeta de trajetórias circulares dos movimentos dos corpos celestes. Isso tudo foi muito bem estudado por Kepler e posteriormente por Newton.

A terceira lei de Kepler enuncia que:"o quadrado do período de um planeta ao redor do Sol é proporcional ao cubo do raio médio da sua órbita".

$\;\frac{T^2}{R^3}=k\;\;\;\;(1)$

mais tarde essa lei mostrou ser uma solução particular da lei da gravitação universal de Newton. Considerando que as órbitas planetárias são elipses de pequena excentricidade e que podemos aproximá-las por círculos, lembrando que a força gravitacional do Sol é a força centrípeta desses movimentos, podemos escrever:

$\;m\omega^2R=\frac{GMm}{R^2}\;\;\;\;(2)$

eliminando a massa do planeta, presente nos dois membros já somos informados de que o que seguirá independe dela.

$\;\omega^2=\frac{GM}{R^3}$

traduzindo a velocidade angular em função do período

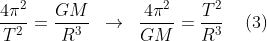
$\;\frac{4\pi^2}{T^2}=\frac{GM}{R^3}\;\;\to\;\;\frac{4\pi^2}{GM}=\frac{T^2}{R^3}\;\;\;\;(3)$

e notamos que o membro da esquerda é uma constante, tal qual previsto por Kepler.

Velocidade angular e período de uma órbita gravitacional

Vamos retomar a equação (2) e verificar esses parâmetros:

em cada órbita gravitacional, para cada corpo, a força centrípeta disponível é constante, pois é a força gravitacional para aquele raio. Então deve haver para cada órbita uma velocidade angular e um período que a tornam possível.

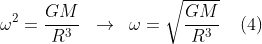
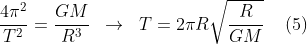
$\;\omega^2=\frac{GM}{R^3}\;\;\to\;\;\omega=\sqrt{\frac{GM}{R^3}}\;\;\;\;(4)$

$\;\frac{4\pi^2}{T^2}=\frac{GM}{R^3}\;\;\to\;\;T=2\pi R\sqrt{\frac{R}{GM}}\;\;\;\;(5)$

Uma órbita Geoestacionária

Nossa equação (5) nos sugere que existe a possibilidade de se manter um satélite numa órbita em que ele possua o mesmo período de rotação da Terra e que fixado esse período, a única variável será o raio dessa órbita.

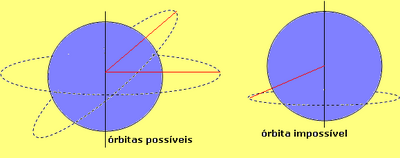
Devemos lembrar que sendo gravitacional a força centrípeta, o centro de qualquer órbita em torno de um planeta ou estrela será o centro de massa do corpo celeste central. Não será possível nenhuma órbita que não tenha esse centro. Com isso fica claro que a única órbita geoestacionária natural possível deve se desenvolver num plano orbital perpendicular ao eixo de rotação da Terra de modo a poder acompanhar sua rotação.

Tomando o raio da Terra como 6370km e o período de 24h teremos, efetuando as conversões necessárias no Sistema Internacional:

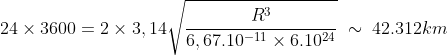
$\;24\times3600=2\times 3,14\sqrt{\frac{R^3}{6,67.10^{-11}\times 6.10^{24}}}\;\sim\;42.312km$

Uma órbita numa altitude aproximada de 35.900km.

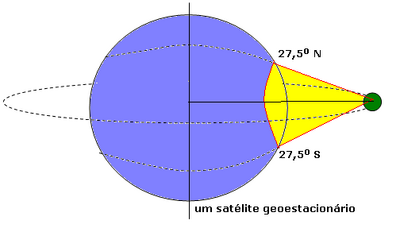
Satélites colocados nessa órbita são chamados geoestacionários pois permanecem relativamente parados sobre o mesmo ponto e são muito utilizados nas telecomunicações e monitoramento climático ou ambiental. Devido à esfericidade da Terra os satélites geoestacionários cobrem um círculo de <math>55^o</math> de latitude sobre a superfície.

A órbita Geossíncrona

Chama-se '''geossíncrona''' a uma órbita qualquer que tenha o mesmo período da rotação do planeta. Sendo assim, a órbita geoestacionária é também geossíncrona, porém só uma das órbitas geossíncronas é geoestacionária. As órbitas geossíncronas em geral são órbitas cuja trajetória é reversa à linha do equador, formando com ela um ângulo conhecido como '''''inclinação da órbita'''''.

Da mesma maneira e pela mesma razão (reveja a equação 5) só há um raio possível para uma órbita geossíncrona. Um satélite nesse tipo de órbita passa metade do tempo no hemisfério norte e metade no hemisfério sul.