 O
Pêndulo
Físico
ou Pêndulo Composto |
Para inteira
compreensão deste assunto você deve ler antes Dinâmica
da Rotação (para o nível
médio)
1. O Pêndulo
Simples
Quando começamos a estudar os pêndulos sempre o
fizemos na
suposição de que eram formados por uma massa de
dimensões desprezíveis presas a fios
inextensíveis
e de massas igualmente desprezíveis.
Isso foi vantajoso, pois pudemos nos concentrar na essência
do
movimento pendular. Isolamos as variáveis que nos
interessava
investigar. Em particular desejávamos conhecer o
período
dos pêndulos que assim eram chamados Pêndulos
Simples.
Vimos
também
quais as forças que atuam no seu movimento e que a
força
centrípeta responsável pelo movimento circular
é a
resultante entre a componente do peso da massa pendular que
é
colinear ao fio (Py)
e a
tração (T) no fio. A
componente tangencial do peso produz a aceleração
tangencial, sempre oposta ao movimento, de maneira que Px é
sempre uma força restauradora.
O pêndulo executa um movimento oscilatório que,
para ângulos muito pequenos 
, é um MHS
cujo
período é dado por
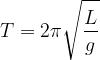
O
pêndulo simples será de boa ajuda no estudo dos
pêndulos reais, ou pêndulos compostos, ou ainda,
pêndulos físicos.
2.
O Pêndulo
Físico
Em todos os pêndulos reais que pudermos contruir as massas
pendulares não serão simples
partículas, mas
possuirão dimensões que nem sempre
serão
deprezíveis, os fios terão massa e muitas vezes
serão substituídos por hastes rígidas
de massas
não desprezíveis. Na verdade, qualquer corpo que
seja
posto a oscilar preso a um ponto fora do seu centro de massa
constituirá um pêndulo.
Nestes
casos a massa já não pode mais ser considerada
pontual.
Sua distribuição em relação
ao eixo de
rotação já é significativa
e precisa ser
considerada sob o ponto de vista da Dinâmica da
Rotação.
Na dinâmica da rotação aprendemos que a
distribuição de massa em
relação ao eixo de
rotação é a responsável
pela inércia
dos corpos nesses casos e recebe o nome de Momento de
Inércia.
O momento de inércia de um sistema em
rotação
é a soma dos momentos de inércia de todos os seus
constituintes.
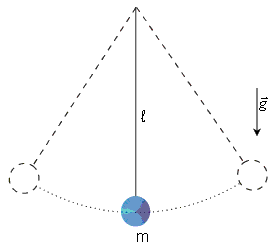
O
pêndulo da figura à direita é muito
comum em alguns
tipos de relógios. Neles uma massa pendular é
fixa a uma
haste rígida. Um sistema de corda aplica uma
força ao
pêndulo de maneira a compensar as perdas por atritos e manter
o
período constante. O movimento do pêndulo aciona
um
sistema de engrenagens que move os ponteiros. Exceto pela energia
adicional para compensar as perdas, este é um
relógio
movido a gravidade.
Para lidar com este tipo de pêndulo precisaremos conhecer a
distância entre o centro de massa do sistema e o centro de
giração. Para isso faremos uma muito pequena
revisão sobre como encontrar o centro de massa de um sistema
de partículas.
3.
A
Posição do Centro de Massa
O centro de massa de um corpo é a
posição pela qual se pendurado ele apresenta um
equilíbrio indiferente. Isto é o mesmo que dizer
que o centro de massa é o ponto em que toda a massa do corpo
estaria concentrada se ele fosse representado por uma
partícula equivalente. Se um corpo apresenta isotropia
em relação à sua massa
específica, isto é, se a sua massa
específica for a mesma em qualquer de seus pontos, o centro
de massa se localiza coincidente com o seu centro geométrico.
A
depender da geometria de um
corpo o seu centro de massa pode mesmo estar fora dele:
Duas
pequenas esferas de
massas iguais a m
separadas por uma distância d, terão seu centro de
massa situado no ponto médio entre elas e isso é
até bastante intuitivo.
Veremos a seguir como calcular a posição do
centro de massa de uma distribuição de
partículas.
Ir
para a página 2
