Da
segunda lei sabemos que uma força faz variar a
aceleração de um corpo. A lei aplica-se na
rotação:


O
disco ao lado gira em relação a um eixo
perpendicular ao
plano que o contém e passante pelo centro. Essa
rotação se dá pela
ação da
força F, ou mais propriamente, pelo momento da
força F em relação ao centro.
Vamos designar esse torque pela letra tau 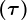 .
.
O torque deve, portanto, fazer variar a velocidade angular do disco em proporção à sua inércia:
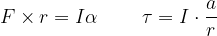 (a)
(a)
em função da aceleração angular ou da aceleração tangencial. De outra forma, vamos agora ver a segunda lei da maneira como Newton a enunciou:
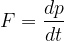 em função da variação do
momento linear em
relação ao tempo. O momento linear se expressa
como
em função da variação do
momento linear em
relação ao tempo. O momento linear se expressa
como 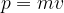 e se estamos supondo uma verdadeira analogia entre as leis da
translação e da rotação,
deve haver algo
equivalente ao momento linear na rotação e, que
antecipadamente, vamos dizer que se chama momento angular.
e se estamos supondo uma verdadeira analogia entre as leis da
translação e da rotação,
deve haver algo
equivalente ao momento linear na rotação e, que
antecipadamente, vamos dizer que se chama momento angular.
O torque deve, portanto, fazer variar a velocidade angular do disco em proporção à sua inércia:
em função da aceleração angular ou da aceleração tangencial. De outra forma, vamos agora ver a segunda lei da maneira como Newton a enunciou:
que é a expressão para o momento angular. Da mesma maneira que o momento linear se conserva na ausência de forças externas, também o momento angular se conserva. Nos dois casos, a variação do momento reflete a ação de uma força externa.
Ainda persistindo na analogia, se a variação do momento linear corresponde à força aplicada, a variação do momento angular deve corresponder ao torque aplicado:
e sendo o momento de inércia constante
a mesma equação (a) que já encontramos anteriormente com um raciocínio diferente.
Parte 3 - Tres exemplos de aplicações
Exemplo 1-

a figura ,
ao lado mostra um
disco de massa M
e raio r
que gira na vertical devido ao corpo de massa m,
sob a
ação da gravidade. (Encontre o momento de
inércia do disco na tabela fornecida).
Calcule:
a) a tração no fio
b) a aceleração do conjunto
Solução:
da mesma maneira que fazíamos na translação, vamos fazer o equacionamento de corpo isolado para o disco e o bloco.
No disco:
a segunda lei aplicada à rotação nos diz que
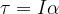 sendo
sendo 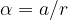 temos
temos
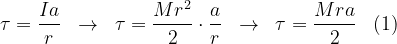
No bloco:
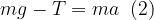
mas, como
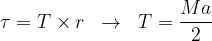
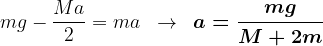
agora a tração é obtida facilmente.
Exemplo 2-
Uma esfera de massa m e raio r rola sem deslizar (a partir do repouso) por um plano horizontal, impulsionada por uma força F, tangente à sua superfície, que atuou por t s. Calcule sua energia cinética total.
Solução:
o rolamento sem deslizamento é um movimento composto por rotação e translação. Logo devemos encontrar a soma das energias cinéticas de translação e de rolamento.
Vimos que o torque aplicado corresponde a uma variação no momento angular
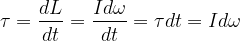
portanto podemos encontrar a variação da velocidade angular que será a velocidade angular final, já que o movimento se inicia a partir do repouso.
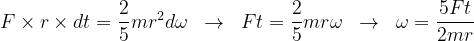
a energia cinética de rotação
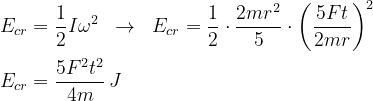
a energia cinética de translação é dada pela energia do centro de massa
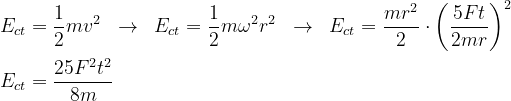
a energia cinética total
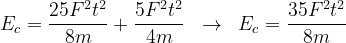
ir para o fórum
Calcule:
a) a tração no fio
b) a aceleração do conjunto
Solução:
da mesma maneira que fazíamos na translação, vamos fazer o equacionamento de corpo isolado para o disco e o bloco.
No disco:
a segunda lei aplicada à rotação nos diz que
No bloco:
mas, como
agora a tração é obtida facilmente.
Exemplo 2-
Uma esfera de massa m e raio r rola sem deslizar (a partir do repouso) por um plano horizontal, impulsionada por uma força F, tangente à sua superfície, que atuou por t s. Calcule sua energia cinética total.
Solução:
o rolamento sem deslizamento é um movimento composto por rotação e translação. Logo devemos encontrar a soma das energias cinéticas de translação e de rolamento.
Vimos que o torque aplicado corresponde a uma variação no momento angular
portanto podemos encontrar a variação da velocidade angular que será a velocidade angular final, já que o movimento se inicia a partir do repouso.
a energia cinética de rotação
a energia cinética de translação é dada pela energia do centro de massa
a energia cinética total
ir para o fórum
