Morgado 1- Geometria

Boa tarde, companheiros.
Estou travado nesta questão do Morgado 1:

Da figura, sabe-se que D é o pé da bissetriz interna do ângulo reto Â. Se DE é perpendicular a BC, o ângulo ^α:
a)É igual a ^c.
b)É igual a (90° + ^c)/2.
c)É igual a 45°.
d)É maior que 45°.

Resposta: letra d.
Agradeço desde já.

não sei desvirar a imagem amigos, desculpe por isso...

Agradeço sua atenção.

dlemos escreveu:

Sei que o tópico é velho mas acredito que a resolução esteja errada e não queria abrir outro para a mesma questão.
theta é a soma dos dois ângulos opostos -> theta > 45 -> não necessariamente x < 45.

Se alguém puder explicar a resolução do dlemos ou postar outra para esta questão, agradeço. Estou a algumas horas tentando resolvê-la sem sucesso.

Tive problemas com a questão também, pesquisei, não encontrei soluções satisfatórias, então continuei tentando e consegui de uma forma que considero fora da proposta da questão, dado o contexto dela, mas é melhor que nada 

Primeiro, é bom lembrar que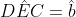

Pelo teorema da bissetriz interna: 
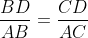 (I)

Pela lei dos senos no : 

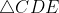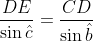
(II)

Pela lei dos senos no :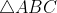 

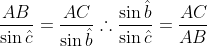(III)

Agora igualando (II) e (III):

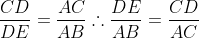(IV)

E agora (I) e (I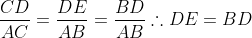V):

(V)

Só com isso já sabemos que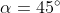 , mas sendo mais "técnico":

Lei dos senos no :

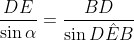(VI) 

Unindo (V) e (VI):



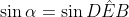
E como são ângulos de um triângulo retângulo:



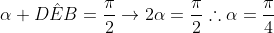
Acho que o gabarito está errado mesmo, e poderia ser resolvida pela congruência dos triângulos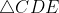 e 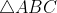, seria mais ou menos a mesma coisa.

Me lembro da época que fiz essa questão no livro. Basta saber um pouco de quadriláteros inscritíveis que logo verá uma circunferência no quadrilátero ABDE. O ângulo alfa enxerga o mesmo arco que o ângulo de 45, logo alfa=45

Faz bastante tempo que perguntaram, mas deixo minha resposta para ajudar aos próximos que tiverem a mesma dúvida

A figura não está mais disponível, depois de tantos anos.
Caso a tenha, poste, por favor, para que os usuários possam entender.