Função composta: Domínio

por Luana Skywalker Ter 30 Ago 2011, 22:25

(UFSCAR)Considere as funções reais f e g, definidas por
f(x)=(x-2)/(sqrt x-2)
g(x)= |3 - 2x| +1

a) Eu fiz cheers

b) não consegui Neutral

Determine o domínio de f(g(x)).

Eu fiz a composta e ficou:

f(g(x))=(|3 - 2x| +1 -2)/(sqrt |3 - 2x| +1 -2)

Bom, o domínio é o x e o x no denominador tem que ser positivo e não pode dar 0, neh?

Então fiz:

Quando módulo for positivo:

3-2x+1-2>0
2-2x>0
x>1

ou

Quando módulo for negativo:

-3+2x+1-2<0
-4<-2x
-2<-x
x<2 (mudei a desigualdade pq multipliquei por -1 nos dois lados)

Porém, o gabarito tá assim:

x<1 ou x>2

É a segunda parte q estou errando, porque? :hfy:

por **abelardo** Qua 31 Ago 2011, 01:14

Mesmo você resolvendo a letra a), é bom que poste a questão, já que as vezes as questões anteriores podem guardar parte da resposta das letras seguintes.

Como o conjunto universo não foi explicitado, então pressupõem-se que estamos trabalhando com $\dpi{120} \mathbb{R}$ .

$\dpi{150} \left\{\begin{matrix} f(x)=\frac{x-2}{\sqrt{x-2}} \\ g(x)=\left | 3-2x \right |+1 \end{matrix}\right.$

$\dpi{150} f(x)=\frac{x-2}{\sqrt{x-2}}=\frac{(x-2)^1}{(x-2)^{\frac{1}{2}}}=(x-2)^{1-\frac{1}{2}}=(x-2)^{\frac{1}{2}}$

$\dpi{120} f(x)=\sqrt{x-2}$ (Lembrando que tudo que está dentro dessa raiz deve ser maior que zero. Não pode ser igual a zero porque assim teríamos uma indeterminação, a divisão por zero)

$\dpi{120} f[g(x)]=\sqrt{g(x)-2}=\sqrt{\left | 3-2x \right |+1-2}=\sqrt{\left | 3-2x \right |-1}$ (Tudo que está dentro da raiz deve ser MAIOR que zero).

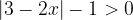
$\dpi{120} \left |3-2x \right |-1>0$
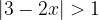
$\dpi{120} \left |3-2x \right |>1$

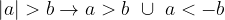
Propriedade blábláblá da desigualdade modular. Se $\dpi{120} \left | a \right |>b \to a>b \ \cup \ a<-b$

$\dpi{120} \left\{\begin{matrix} 3-2x >1\\ \ \ 3-2x <-1 \end{matrix}\right.$

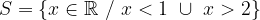
Resolvendo, temos que $\dpi{120} S=\left \{ x \in \mathbb{R} \ / \ x<1 \ \cup \ x>2 \right \}$

por **abelardo** Qua 31 Ago 2011, 01:17

O seu erro foi nas propriedades do módulo.

por Luana Skywalker Qua 31 Ago 2011, 06:30

abelardo escreveu:O seu erro foi nas propriedades do módulo.

Sim.

Eu pensava q fosse assim:

|3-2x|

Ele pode ser positivo ou negativo, neh?

Então no caso positivo sai ele mesmo:

3-2x

e
no caso de ser negativo sai seu oposto

-3+2x

Obrigada! Very Happy

por **abelardo** Qua 31 Ago 2011, 09:22

Luana Skywalker escreveu:(UFSCAR)Considere as funções reais f e g, definidas por
f(x)=(x-2)/(sqrt x-2)
g(x)= |3 - 2x| +1

a) Eu fiz

b) não consegui

Determine o domínio de f(g(x)).

Eu fiz a composta e ficou:

f(g(x))=(|3 - 2x| +1 -2)/(sqrt |3 - 2x| +1 -2)

Bom, o domínio é o x e o x no denominador tem que ser positivo e não pode dar 0, neh?

Então fiz:

Quando módulo for positivo (Para x<3/2):

3-2x+1-2>0
2-2x>0
-2x > -2 (Cuidado com o sinal, você esqueceu da mudança)

x<1, mas x deve ser menor que 3/2, logo x<1

ou

Quando módulo for negativo (Para x>3/2):

-3+2x+1-2<0
-4<-2x
-2<-x
x>2 (mudei a desigualdade pq multipliquei por -1 nos dois lados) (Não mudou o sinal)

x>2 e x deve ser maior que 3/2, logo x>2.
Porém, o gabarito tá assim:

x<1 ou x>2

É a segunda parte q estou errando, porque? :hfy:

por Luana Skywalker Sex 02 Set 2011, 02:39

Muito Obrigada!!! Eu vou estudar mais sobre módulo, tb tenho uma aula de Função Modular para fazer, aqueles gráficos são bem loucos

por **abelardo** Sex 02 Set 2011, 02:45

Realmente, quando se estuda a primeira vez sobre funções modulares (antes só se vê, normalmente, função do primeiro e do segundo grau) vê-se uma diferença na construção dos gráficos. As vezes as funções definidas por mais de uma sentença apresentam gráficos bem engraçados, lembram figuras do cotidiano.