Tronco de cone
3 participantes
Página 1 de 1
 Tronco de cone
Tronco de cone
As bases de um tronco de cone circular reto são círculos de raios 6 cm e 3 cm. Sabendo-se que a área lateral do tronco é igual à soma das áreas das bases, calcule:
a) a altura do tronco de cone;
b) o volume do tronco de cone.
R: a) 4cm b) 84pi cm³
a) a altura do tronco de cone;
b) o volume do tronco de cone.
R: a) 4cm b) 84pi cm³

Matheus José- Mestre Jedi

- Mensagens : 630
Data de inscrição : 29/10/2015
Idade : 25
Localização : Santos
 Re: Tronco de cone
Re: Tronco de cone
Boa tarde Matheus.
Qual sua dúvida? Sabendo as equações, ou o teorema de Pappus-Guldin, não há mistério.
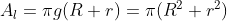
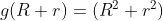 (encontre g)
(encontre g)
Teorema de Pitágoras no tronco de cone:
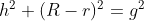 ... (encontre h)
... (encontre h)
Volume do tronco de cone:
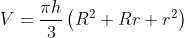
Qual sua dúvida? Sabendo as equações, ou o teorema de Pappus-Guldin, não há mistério.
Teorema de Pitágoras no tronco de cone:
Volume do tronco de cone:

gilberto97- Fera

- Mensagens : 587
Data de inscrição : 12/03/2014
Idade : 26
Localização : São Luís, Maranhão, Brasil
 Re: Tronco de cone
Re: Tronco de cone
H = altura do tronco de cone
h = altura do conezinho retirado do cone original para formar o tronco
g, G = geratrizes do conezinho e do cone original
R = 6, r = 3
h/r = (H + h)/R ---> h/3 (H + h)/6 ---> h = H
g² = h² + r² ---> g² = H² + 9 ---> g = √(H² + 9)
G = 2.g ---> G = 2.√(H² + 9)
Sl = pi.R.G - pi.r.g ---> Sl = 9.√(H² + 9)
Sb = pi.R² + pi.r² ---> Sb = 45.pi
9.√(H² + 9) = 45.pi ---> H² + 9 = 25 ---> H = 4
Complete
h = altura do conezinho retirado do cone original para formar o tronco
g, G = geratrizes do conezinho e do cone original
R = 6, r = 3
h/r = (H + h)/R ---> h/3 (H + h)/6 ---> h = H
g² = h² + r² ---> g² = H² + 9 ---> g = √(H² + 9)
G = 2.g ---> G = 2.√(H² + 9)
Sl = pi.R.G - pi.r.g ---> Sl = 9.√(H² + 9)
Sb = pi.R² + pi.r² ---> Sb = 45.pi
9.√(H² + 9) = 45.pi ---> H² + 9 = 25 ---> H = 4
Complete

Elcioschin- Grande Mestre

- Mensagens : 71603
Data de inscrição : 15/09/2009
Idade : 77
Localização : Santos/SP
 Re: Tronco de cone
Re: Tronco de cone
Gilberto, não conhecia essas equações,só conheço a último do volume, de onde veio elas ? o.o'
Consegui resolver o problema, obrigado Gilberto e Elcio.
Minha dúvida era sobre como encontrar a altura.
Consegui resolver o problema, obrigado Gilberto e Elcio.
Minha dúvida era sobre como encontrar a altura.

Matheus José- Mestre Jedi

- Mensagens : 630
Data de inscrição : 29/10/2015
Idade : 25
Localização : Santos
 Re: Tronco de cone
Re: Tronco de cone
A área lateral do tronco de cone... Se você conhece o teorema de Pappus-Guldin, pode derivar facilmente várias equações de áreas da geometria espacial. É útil para calcular áreas laterais. Veja:Matheus José escreveu:Gilberto, não conhecia essas equações,só conheço a último do volume, de onde veio elas ? o.o'
Consegui resolver o problema, obrigado Gilberto e Elcio.
Minha dúvida era sobre como encontrar a altura.

(Fonte: http://www.alfaconnection.pro.br/matematica/geometria/superficies-e-solidos-de-revolucao/superficies-de-revolucao/)
Onde
É lógico que existem outros meios, mais simples até, de se chegar à equação da área lateral do tronco de cone, mas é sempre bom ter várias armas.

gilberto97- Fera

- Mensagens : 587
Data de inscrição : 12/03/2014
Idade : 26
Localização : São Luís, Maranhão, Brasil
 Re: Tronco de cone
Re: Tronco de cone
Obrigado pelas explicações.

Matheus José- Mestre Jedi

- Mensagens : 630
Data de inscrição : 29/10/2015
Idade : 25
Localização : Santos
 Tópicos semelhantes
Tópicos semelhantes» Volume tronco de cone e cone de mesma altura
» Cone e Tronco de Cone
» Cone em um tronco de cone
» Cone
» Cone!
» Cone e Tronco de Cone
» Cone em um tronco de cone
» Cone
» Cone!
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|













